Question

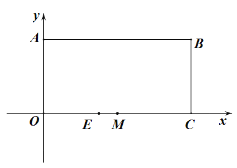
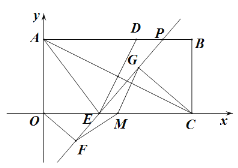
【题目】如图，矩形OABC的顶点A的坐标（0,4），C的坐标为（8,0），把矩形折叠，使点C与点A重合，折痕为DE．

求出点E的坐标．

（2）点M为OC的中点，点P为线段AB上一动点，作直线EP，分别过点O、C作直线EP的垂线，垂足分别为点F、G．求证：MF=MG

（3）在（2）的条件下，当△FMG为等腰直角三角形时，请直接写出此时直线EP的表达式．

Answer 1

【答案】（1）详见解析；E（3，0）；（2）详见解析；（3）.

【解析】

（1）依据折叠的性质即可求解；

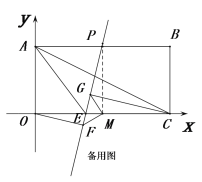
（2）延长OF交GM的延长线于点N，可得△OMN≌△CMG，即可证明MF=MG.

（3）△FMG为等腰直角三角形，求出F点的坐标，在结合E，F的坐标求EP的解析式.

（1）略.E（3，0）

（2）证明：如图，延长OF交GM的延长线于点N，可得△OMN≌△CMG，

得 MN=MG，即可得MF=MG.

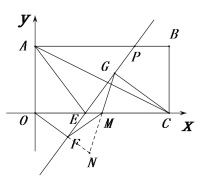
（3）