题目内容
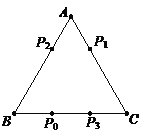
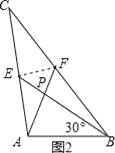
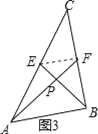
【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
特例探索
(1)如图1,当∠ABE=45°,c=![]() 时,a= ,b= ;
时,a= ,b= ;
如图2,当∠ABE=30°,c=4时,a= ,b= ;

归纳证明
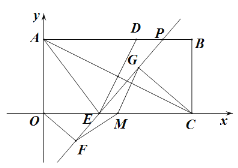
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
拓展应用
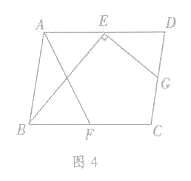
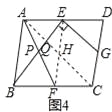
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=![]() ,AB=3.求AF的长.
,AB=3.求AF的长.
【答案】(1)2![]() ,2
,2![]() ;2
;2![]() ,2
,2![]() ;(2)
;(2)![]() +
+![]() =5
=5![]() ;(3)AF=4.
;(3)AF=4.
【解析】
试题(1)∵AF⊥BE,∠ABE=45°,∴AP=BP=![]() AB=2,∵AF,BE是△ABC的中线,∴EF∥AB,EF=
AB=2,∵AF,BE是△ABC的中线,∴EF∥AB,EF=![]() AB=
AB=![]() ,∴∠PFE=∠PEF=45°,∴PE=PF=1,在Rt△FPB和Rt△PEA中,AE=BF=
,∴∠PFE=∠PEF=45°,∴PE=PF=1,在Rt△FPB和Rt△PEA中,AE=BF=![]() =
=![]() ,∴AC=BC=2
,∴AC=BC=2![]() ,∴a=b=2
,∴a=b=2![]() ,如图2,连接EF,同理可得:EF=
,如图2,连接EF,同理可得:EF=![]() ×4=2,∵EF∥AB,∴△PEF~△ABP,∴
×4=2,∵EF∥AB,∴△PEF~△ABP,∴![]() ,在Rt△ABP中,AB=4,∠ABP=30°,∴AP=2,PB=2
,在Rt△ABP中,AB=4,∠ABP=30°,∴AP=2,PB=2![]() ,∴PF=1,PE=
,∴PF=1,PE=![]() ,在Rt△APE和Rt△BPF中,AE=
,在Rt△APE和Rt△BPF中,AE=![]() ,BF=
,BF=![]() ,∴a=2
,∴a=2![]() ,b=2
,b=2![]() ,故答案为:2
,故答案为:2![]() ,2
,2![]() ,2
,2![]() ,2
,2![]() ;
;
(2)猜想:a2+b2=5c2,如图3,连接EF,设∠ABP=α,∴AP=csinα,PB=ccosα,由(1)同理可得,PF=![]() PA=
PA=![]() ,PE=
,PE=![]() =
=![]() ,AE2=AP2+PE2=c2sin2α+
,AE2=AP2+PE2=c2sin2α+![]() ,BF2=PB2+PF2=
,BF2=PB2+PF2=![]() +c2cos2α,∴
+c2cos2α,∴![]() =c2sin2α+
=c2sin2α+![]() ,
,![]() =
=![]() +c2cos2α,∴
+c2cos2α,∴![]() +
+![]() =
=![]() +c2cos2α+c2sin2α+
+c2cos2α+c2sin2α+![]() ,∴a2+b2=5c2;
,∴a2+b2=5c2;
(3)如图4,连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,∵点E、G分别是AD,CD的中点,∴EG∥AC,∵BE⊥EG,∴BE⊥AC,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=2![]() ,∴∠EAH=∠FCH,∵E,F分别是AD,BC的中点,∴AE=
,∴∠EAH=∠FCH,∵E,F分别是AD,BC的中点,∴AE=![]() AD,BF=
AD,BF=![]() BC,∴AE=BF=CF=
BC,∴AE=BF=CF=![]() AD=
AD=![]() ,∵AE∥BF,∴四边形ABFE是平行四边形,∴EF=AB=3,AP=PF,在△AEH和△CFH中,
,∵AE∥BF,∴四边形ABFE是平行四边形,∴EF=AB=3,AP=PF,在△AEH和△CFH中,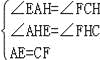 ,∴△AEH≌△CFH,∴EH=FH,∴EQ,AH分别是△AFE的中线,由(2)的结论得:AF2+EF2=5AE2,∴AF2=5
,∴△AEH≌△CFH,∴EH=FH,∴EQ,AH分别是△AFE的中线,由(2)的结论得:AF2+EF2=5AE2,∴AF2=5![]() ﹣EF2=16,∴AF=4.
﹣EF2=16,∴AF=4.

 阅读快车系列答案
阅读快车系列答案