题目内容
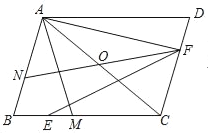
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( ) 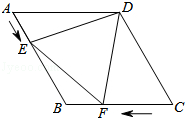
A.1
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:连接BD, 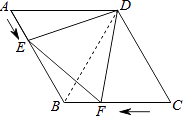
∵四边形ABCD是菱形,
∴AB=AD,∠ADB= ![]() ∠ADC=60°,
∠ADC=60°,
∴△ABD是等边三角形,
∴AD=BD,
又∵△DEF是等边三角形,
∴∠EDF=∠DEF=60°,
又∵∠ADB=60°,
∴∠ADE=∠BDF,
∴△ADE和△BDF中, 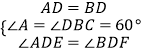 ,
,
∴△ADE≌△BDF,
∴AE=BF,
∵AE=t,CF=2t,
∴BF=BC﹣CF=4﹣2t,
∴t=4﹣2t
∴t= ![]()
故选D.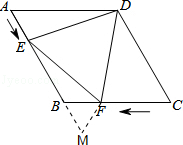
延长AB至M,使BM=AE,连接FM,证出△DAE≌EMF,得到△BMF是等边三角形,再利用菱形的边长为4求出时间t的值.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目