题目内容
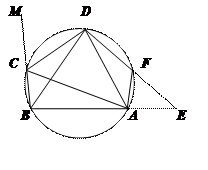
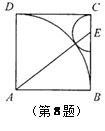
(本题满分10分)如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心,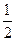 AC长为半径作
AC长为半径作 ⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.
⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.
(1)求证:D是 弧AE 的中点;
(2)求证:∠DAO =∠B+∠BAD;
(3)若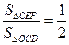 ,且AC=4,求CF的长.
,且AC=4,求CF的长.
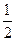 AC长为半径作
AC长为半径作 ⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.
⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.(1)求证:D是 弧AE 的中点;
(2)求证:∠DAO =∠B+∠BAD;
(3)若
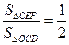 ,且AC=4,求CF的长.
,且AC=4,求CF的长.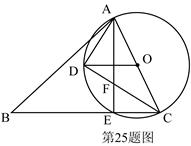 |
(本题满分10分)
证明:(1)∵AC是⊙O的直径
∴AE⊥BC …………1分
∵OD∥BC
∴AE⊥OD …………2分
∴D是 的中点 …………3分
的中点 …………3分
(2)方法一:
如图,延长OD交AB于G,则OG∥BC …4分
∴∠AGD=∠B
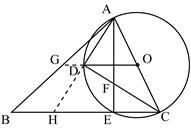 ∵∠ADO=∠BAD+∠AGD …………5分
∵∠ADO=∠BAD+∠AGD …………5分
又∵OA=OD
∴∠DAO=∠ADO
∴∠DAO=∠B+∠BAD …………6 分
分
方法二:
如图,延长AD交BC于H …4分
则∠ADO=∠AHC
∵∠AHC=∠B+∠BAD …………5分
∴∠ADO =∠B+∠BAD
=∠B+∠BAD
又∵OA=OD
∴∠DAO=∠B+∠BAD …………6分
(3) ∵AO=OC ∴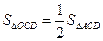
∵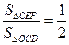 ∴
∴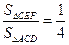 …………7分
…………7分
∵∠ACD=∠F CE ∠ADC=∠FEC=90°
CE ∠ADC=∠FEC=90°
∴△ACD∽△FCE …………………8分
∴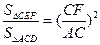 即:
即: 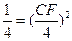 …………9分
…………9分
∴CF="2 " …………10分
证明:(1)∵AC是⊙O的直径
∴AE⊥BC …………1分
∵OD∥BC
∴AE⊥OD …………2分
∴D是
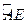 的中点 …………3分
的中点 …………3分(2)方法一:
如图,延长OD交AB于G,则OG∥BC …4分
∴∠AGD=∠B
 ∵∠ADO=∠BAD+∠AGD …………5分
∵∠ADO=∠BAD+∠AGD …………5分又∵OA=OD
∴∠DAO=∠ADO
∴∠DAO=∠B+∠BAD …………6
 分
分方法二:
如图,延长AD交BC于H …4分
则∠ADO=∠AHC
∵∠AHC=∠B+∠BAD …………5分
∴∠ADO
 =∠B+∠BAD
=∠B+∠BAD 又∵OA=OD
∴∠DAO=∠B+∠BAD …………6分
(3) ∵AO=OC ∴
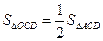
∵
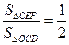 ∴
∴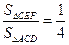 …………7分
…………7分∵∠ACD=∠F
 CE ∠ADC=∠FEC=90°
CE ∠ADC=∠FEC=90°∴△ACD∽△FCE …………………8分
∴
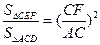 即:
即: 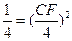 …………9分
…………9分∴CF="2 " …………10分
略

练习册系列答案
相关题目

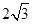 cm,则OA= cm.
cm,则OA= cm.