题目内容
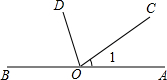如图，已知∠1=34°40′，OD平分∠BOC，求∠AOD的度数．
解：∵∠1=34°40′，
∴∠BOC=180°-∠1=145°20′，
∵OD平分∠BOC，
∴∠DOC=
∠BOC=72°40′，
∴∠AOD=∠DOC+∠1=72°40′+34°40′=107°20′．
分析：求出∠BOC，根据角平分线求出∠DOC，求出∠1+∠DOC即可．
点评：本题考查了邻补角，角平分线的应用，关键是求出∠DOC的度数．
∴∠BOC=180°-∠1=145°20′，
∵OD平分∠BOC，
∴∠DOC=
∠BOC=72°40′，∴∠AOD=∠DOC+∠1=72°40′+34°40′=107°20′．
分析：求出∠BOC，根据角平分线求出∠DOC，求出∠1+∠DOC即可．
点评：本题考查了邻补角，角平分线的应用，关键是求出∠DOC的度数．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
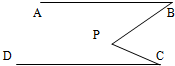10、如图，已知AB∥CD，∠ABP=34°，∠DCP=27°，那么∠BPC=
（2012•铜仁地区）如图，定义：在直角三角形ABC中，锐角α的邻边与对边的比叫做角α的余切，记作ctanα，即ctanα=
如图，已知AB⊥CD，△ABD，△BCE都是等腰直角三角形，如果CD=8，BE=3，则AC等于（ ）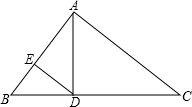
如图，已知直角△ABC中，∠BAC=90°，∠B=56°，AD⊥BC，DE∥CA．∠ADE的度数为（ ）