题目内容
如图，已知AB⊥CD，△ABD，△BCE都是等腰直角三角形，如果CD=8，BE=3，则AC等于（ ）分析：由于△BCE是等腰直角三角形，那么可得BC=BE=3，而DC=8，可求DB=5，又∵△ABD是等腰直角三角形，那么可知AB=5，在Rt△ABC中，利用勾股定理可求AC．
解答：解：∵△BCE是等腰直角三角形，
∴BC=BE=3，
又∵CD=BD+BC=8，
∴BD=5，
∵△ABD是等腰直角三角形，
∴AB=BD=5，
在Rt△ABC中，AC=
=
=
．
故选D．
∵△BCE是等腰直角三角形，∴BC=BE=3，
又∵CD=BD+BC=8，
∴BD=5，
∵△ABD是等腰直角三角形，
∴AB=BD=5，
在Rt△ABC中，AC=
| AB2+BC2 |
| 32+52 |
| 34 |
故选D．
点评：本题考查了等腰直角三角形的性质、勾股定理，解题的关键是分别求出BC、AB．
练习册系列答案
相关题目
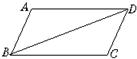15、如图，已知AB=CD且∠ABD=∠BDC，要证∠A=∠C，判定△ABD≌△CDB的方法是（ ）
如图，已知AB∥CD，∠1=50°25′，则∠2的大小是
如图，已知 AB∥CD，∠A=53°，则∠1的度数是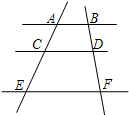
如图，已知AB∥CD∥EF，那么下列结论中，正确的是（ ）