题目内容
【题目】在四边形ABCD中,对角线AC与BD交于点O,E是OC上任意一点,AG⊥BE于点G,交直线BD于点F.

(1)如图1,若四边形ABCD是正方形,判断AF与BE的数量关系:AF与BE的数量关系是 ;
(2)如图2,若四边形ABCD是菱形,∠ABC=120°,求![]() 的值;
的值;
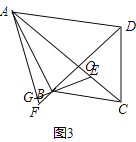
(3)如图3,若四边形ABCD中,AC⊥BD,∠ABC=α,∠DBC=β,请你补全图形,并直接写出:![]() = (用含α,β的式子表示).
= (用含α,β的式子表示).
【答案】(1)AF=BE(2)![]() (3)tan(α﹣β)
(3)tan(α﹣β)
【解析】
试题分析:(1)根据正方形的性质和全等三角形的性质即可得到结论;
(2)根据四边形ABCD是菱形和∠ABC=120°,推出AC⊥BD,∠ABO=60°,根据余角的性质得到∠AFO=∠BEA,又因为∠AOF=∠BOE=90°,推出三角形相似,即可得到结论;
(3)根据垂直的定义得到∠AGB=∠AOB=90°,推出A,G,B,O四点共圆,根据圆内接四边形的性质得到∠GAO=∠GAO,推出△AOF∽△BOE,即可得到结论.
解:(1)AF=BE;
∵四边形ABCD是正方形,
∴∠AOB=∠BOC=90°,AO=BO,
∵AG⊥BE,∠AFO=∠BFG,
∴∠FAO=∠FBG,
在△AFO与△BFO中,
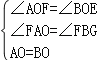 ,
,
∴△AFO≌△BFO,
∴AF=BE;
故答案为:AF=BE;
(2)∵四边形ABCD是菱形,∠ABC=120°,
∴AC⊥BD,∠ABO=60°,
∴∠FAO+∠AFO=90°,
∵AG⊥BE,
∴∠EAG+∠BEA=90°,
∴∠AFO=∠BEA,
又∵∠AOF=∠BOE=90°,
∴△AOF∽△BOE,
∴![]() =
=![]() ,
,
∵∠ABO=60°,AC⊥BD,
∴![]() =tan60°=
=tan60°=![]() ,
,
∴![]() =
=![]() ;
;
(3)如图3,∵AG⊥BE,AC⊥BD,
∴∠AGB=∠AOB=90°,
∴A,G,B,O四点共圆,
∴∠GAO=∠GAO,
∴∠AOF=∠BOE=90°,
∴△AOF∽△BOE,
∴![]() =
=![]() ,
,
∵∠ABO=∠ABC﹣∠OBC=α﹣β,AC⊥BD,
∴![]() =tan(α﹣β),
=tan(α﹣β),
∴![]() =tan(α﹣β).
=tan(α﹣β).
故答案为:tan(α﹣β).

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案