题目内容
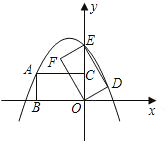
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,AB=4,∠DAB=120°,动点P从点A出发,以每秒2个单位的速度沿AC向终点C运动.过P作PE⊥AB交AB于点E,作PF⊥AD交AD于点F,设四边形AEPF与△ABD的重叠部分的面积为S,点P的运动时间为t.
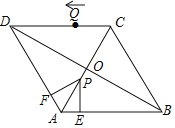
(1)用含t的代数式表示线段BE的长;
(2)当点P与点O重合时,求t的值;
(3)求S与t之间的函数关系式;
(4)在点P出发的同时,有一点Q从点C出发,以每秒6个单位的速度沿折线C﹣D﹣A﹣B运动,设点Q关于AC的对称点是Q',直接写出PQ'与菱形ABCD的边垂直时t的值.
【答案】(1)BE=4﹣t;(2)t=1;(3)当0<t≤1时![]() ,当1<t≤2时,
,当1<t≤2时,![]() ;(4)t的值为
;(4)t的值为![]() s或
s或![]() s或
s或![]() s
s
【解析】
(1)解直角三角形求出AE即可解决问题.
(2)根据PA=OA,构建方程即可解决问题.
(3)分两种情形分别画出图形解决问题即可.
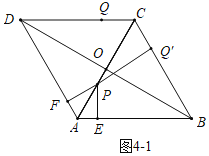
(4)分三种情形:①如图4﹣1中,当PQ′⊥BC时.②如图4﹣2中,当点Q与点F重合时.③如图4﹣3中,当点Q与点E重合时,分别求解即可.
解:(1)如图1中,
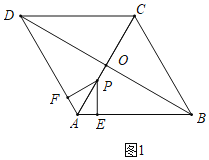
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠CAD=∠CAB=![]() ∠DAB=60°,
∠DAB=60°,
∴△ADC,△ABC都是等边三角形,
∵PE⊥AB,PA=2t,
∴∠PEA=90°,∠APE=30°,
∴AE=![]() PA=t,
PA=t,
∴BE=AB﹣AE=4﹣t.
(2)当点P与点O重合时,PA=OA=2=2t,
∴t=1时,点P与点O重合.
(3)当0<t≤1时,如图1中,重叠部分是四边形PEAF,S=2×![]() ×t×
×t×![]() t=
t=![]() t2.
t2.
当1<t≤2时,如图2中,重叠部分是五边形AEMNF,S=S四边形PEAF﹣S△PMN=![]() t2﹣
t2﹣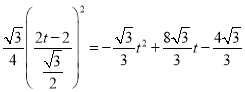 .
.
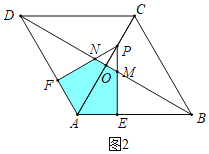
(4)如图4﹣1中,当PQ′⊥BC时,易知PC=2CQ′,可得4﹣2t=2×6t,解得t=![]() .
.
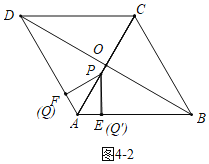
如图4﹣2中,当点Q与点F重合时,PQ⊥AB,则有:6t+t=8,t=![]()
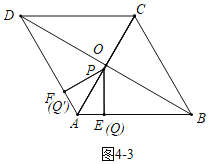
如图4﹣3中,当点Q与点E重合时,PQ′⊥AD,则有:6t=8+t,t=![]() ,
,
综上所述,满足条件的t的值为![]() s或
s或![]() s或
s或![]() s.
s.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】河西中学九年级共有9个班,300名学生,学校要对该年级学生数学学科学业水平测试成绩进行抽样分析,请按要求回答下列问题:
收集数据
(1)若从所有成绩中抽取一个容量为36的样本,以下抽样方法中最合理的是 .
①在九年级学生中随机抽取36名学生的成绩;
②按男、女各随机抽取18名学生的成绩;
③按班级在每个班各随机抽取4名学生的成绩.
整理数据
(2)将抽取的36名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图如下.请根据图表中数据填空:
①C类和D类部分的圆心角度数分别为 °、 °;
②估计九年级A、B类学生一共有 名.
成绩(单位:分) | 频数 | 频率 |
A类(80~100) | 18 |
|
B类(60~79) | 9 |
|
C类(40~59) | 6 |
|
D类(0~39) | 3 |
|
分析数据
(3)教育主管部门为了解学校教学情况,将河西、复兴两所中学的抽样数据进行对比,得下表:
学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
河西中学 | 71 | 52 | 432 | 0.75 |
复兴中学 | 71 | 80 | 497 | 0.82 |
你认为哪所学校本次测试成绩较好,请说明理由.