��Ŀ����
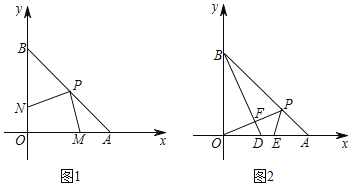
����Ŀ����10�֣����⣺��ͼ��1������Rt��ACB�У���ACB=90�㣬AC=CB����DCE=45������̽��AD��DE��EB����ĵ�����ϵ��

[̽������]
С��ͬѧ����ͼ�α任������CAD�Ƶ�C��ʱ����ת90���õ���CBH������EH������֪�����á�EBH=90�㣬��ECH=��ECB+��BCH=��ECB+��ACD=45�����������߽DZ�������֤��CEH�� ����EH=ED��
��Rt��HBE�У��� �������ɵ�BH2+EB2=EH2����BH=AD���ɵ�AD��DE��EB֮��ĵ�����ϵ�� ��
[ʵ������]
��1����ͼ��2������������ABCD�У���AEF�Ķ���E��F�ֱ���BC��CD���ϣ���AG�������εı߳���ȣ����EAF�Ķ�����
��2���ڣ�1�������£�����BD���ֱ�AE��AF�ڵ�M��N����BE=2��DF=3��BM=2![]() ������С��ͬѧ̽���Ľ��ۣ��������εı߳���MN�ij�.
������С��ͬѧ̽���Ľ��ۣ��������εı߳���MN�ij�.
���𰸡���CDE�����ɣ�![]() ��45�㣻MN=
��45�㣻MN=![]() ��
��
��������
���⣨1���������ε����ʺ�ȫ�������ε��ж�������֤��Rt��ABE��Rt��AGE��Rt��ADF��Rt��AGF����ȫ�������ε����ʼ��������EAF�Ķ�����
��2���ɣ�1��֪��Rt��ABE��Rt��AGE��Rt��ADF��Rt��AGF����AG=x����CE=x��2��CF=x��3����Ϊ![]() ���õ�
���õ�![]() ����������̣����x��ֵ���ɵõ�AG=6���ڣ�2���У�MN2=MB2+ND2��MN=a��
����������̣����x��ֵ���ɵõ�AG=6���ڣ�2���У�MN2=MB2+ND2��MN=a��![]() �����a��ֵ���������MN�ij���
�����a��ֵ���������MN�ij���
����������������߽DZ�������֤��CEH�ա�CDE����EH=ED����Rt��HBE�У��ɹ��ɶ������ɵ�![]() ����BH=AD���ɵ�AD��DE��EB֮��ĵ�����ϵ��
����BH=AD���ɵ�AD��DE��EB֮��ĵ�����ϵ��![]() ���ʴ�Ϊ����CDE�����ɣ�
���ʴ�Ϊ����CDE�����ɣ�![]() ��
��
��1����Rt��ABE��Rt��AGE�У���AB=AG��AE=AE����Rt��ABE��Rt��AGE��HL�������BAE=��GAE��ͬ����Rt��ADF��Rt��AGF�����GAF=��DAF�����ı���ABCD�������Σ����BAD=90�������EAF=![]() ��BAD=45����
��BAD=45����
��2���ɣ�1��֪��Rt��ABE��Rt��AGE��Rt��ADF��Rt��AGF����BE=EG=2��DF=FG=3����EF=5����AG=x����CE=x��2��CF=x��3����![]() ����
����![]() ����������̣���x=6��x=��1����ȥ������AG=6����BD=
����������̣���x=6��x=��1����ȥ������AG=6����BD=![]() =
=![]() =
=![]() ����AB=6����
����AB=6����![]() ����MN=a����
����MN=a����![]() ������a=
������a=![]() ����MN=
����MN=![]() ��
��

 ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ͬ����ϰ����ʦ����ѧ������ϵ�д�
ͬ����ϰ����ʦ����ѧ������ϵ�д� ����ϰ�⽭��ϵ�д�
����ϰ�⽭��ϵ�д�