��Ŀ����
����Ŀ�����ڣ�С����С����μ���ԽҰ�ܱ�������֪����ͬʱ�������Ը��Ե��ٶ������ܲ�ǰ��������һ��ʱ���С�����岻�ʣ�ͣ������Ϣ��1���ӣ�����ԭ�ټ����ܲ�ǰ������С�������յ��������·����ȥ��С�����������С��������ԭ�����ٶ��ܲ�ǰ���յ㣬1���Ӻ��յ㣮��֪���˼�ľ���y��m���������˶�ʱ��x��s���仯��ͼ���ʣ���С����һ�ε����յ�ʱ��С����յ�ľ���Ϊ_____m��

���𰸡�280m
��������
����x=120ʱ��y=60��������·�̵����ٶȲ������ʱ�䣬�ó�С����С������ٴ�С��ϵ��������x=360ʱ��y=0���ó�С����С����ʱ���120��360֮���·�̹�ϵΪ��С����![]() s���ߵ�·�̼���
s���ߵ�·�̼���![]() ����С��
����С��![]() s���ߵ�·�̣��ó�С����С���ٶ�֮��ĵڶ�����ϵʽ�������������ɽ��С����С����ٶȣ���������������ʱ�����С������ʱ�ߵ�·�̣��������ʱ�����յ��·�̣������ó�ȫ�̳�����ȫ�̵ó�С����һ�ε����յ��ʱ�䣬�Ӷ������ʱС�����յ�ľ��룮
s���ߵ�·�̣��ó�С����С���ٶ�֮��ĵڶ�����ϵʽ�������������ɽ��С����С����ٶȣ���������������ʱ�����С������ʱ�ߵ�·�̣��������ʱ�����յ��·�̣������ó�ȫ�̳�����ȫ�̵ó�С����һ�ε����յ��ʱ�䣬�Ӷ������ʱС�����յ�ľ��룮
�⣺��С����С����ٶȷֱ�ΪV1m/s��V2m/s��
��ͼ���֪����x��120sʱ��y��60m��
��120��V1��V2����60
��V1��V2+0.5 ��
�ߵ�x��360ʱ��y��0����С�����岻�ʣ�ͣ������Ϣ��1���ӣ�����ԭ�ټ����ܲ�ǰ����
��60+��360��120��60��V1����360��120��V2��
�ɢ٢ڽ��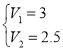
��960��ʱ����������
��ʱС���·����2.5��960��2400m
�����յ��·��Ϊ3��60��180m
��ȫ��Ϊ2400+180��2580m
С����һ�ε����յ��ʱ�䣺![]() +60��920s
+60��920s
��ʱС������յ㣺2580��920��2.5��280m
�ʴ�Ϊ��280m

����Ŀ��ij���мƻ������ס���������Ʒ��������Ʒ�Ľ��ۡ��ۼ����±���
��Ʒ | �� | �� |
���ۣ�Ԫ/���� |
|
|
�ۼۣ�Ԫ/���� | 200 | 100 |
����360Ԫ����������Ʒ�ļ�������180Ԫ����������Ʒ�ļ�����ͬ��
��1����ס���������Ʒ�Ľ����Ƕ���Ԫ��
��2�����������ۼס���������Ʒ��50�����������ۼ�����ƷΪ![]() ����
����![]() ������������50���ס���������Ʒ��������Ϊ
������������50���ס���������Ʒ��������Ϊ![]() Ԫ����
Ԫ����![]() ��
��![]() ֮��ĺ�����ϵʽ�������
֮��ĺ�����ϵʽ�������![]() ����Сֵ��
����Сֵ��





