题目内容
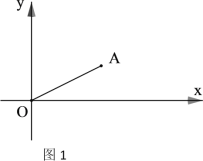
【题目】如图1,在平面直角坐标系中,已知A(a,b),且a.b满足![]() ,
,
(1)求A点的坐标及线段OA的长度;(2)点P为x轴正半轴上一点,且△AOP是等腰三角形,求P点的坐标;
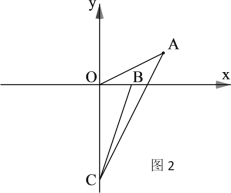
(3)如图2,若B(1,0),C(0,-3),试确定∠ACO+∠BCO的值是否发生变化,若不变,求其值;若变化,请求出变化范围。
【答案】(1)![]() ;(2)P(
;(2)P(![]() ,0)或P(4,0)、P(
,0)或P(4,0)、P(![]() ,0);(3)45.
,0);(3)45.
【解析】
(1)先由二次根式有意义的条件得出a的值,再代入等式得出b的值,从而得出点A的坐标,继而利用两点间的距离公式可得OA的长;
(2)分OA=OP、AO=AP、PO=PA三种情况,利用等腰三角形的性质逐一求解可得;
(3)在x轴负半轴上取一点,使得OD=OB=1,知点B与点D关于y轴对称,据此得∠BCO=∠DCO,根据两点间的距离公式知AD2=10,CD2=10,AC2=20,依据勾股定理逆定理判断出△ACD是等腰直角三角形,利用∠ACO+∠BCO=∠ACO+∠DCO=∠ACD可得答案.
解:
(1)∵![]() ,
,
∴a=2,
则b=1,
∴A(2,1),
则OA=![]() =
=![]() ;
;
(2)当OA=OP时,P(![]() ,0);
,0);
当AO=AP时,如图1,作AH⊥x轴于点H,
则OH=PH=2,
∴OP=4,
∴P(4,0);
当P′O=P′A时,设P′O=P′A=x,则P′H=2-x,

由AP′2=P′H2+AH2得(2-x)2+12=x2,
解得:x=![]() ,
,
∴P(![]() ,0).
,0).
(3)如图2,在x轴负半轴上取一点,使得OD=OB=1,

则点B与点D关于y轴对称,
∴∠BCO=∠DCO,
∵A(2,1),D(-1,0),C(0,-3),
∴AD2=32+12=10,CD2=12+32=10,AC2=22+42=20,
∴AD2+CD2=AC2,且AD=CD,
∴△ACD是等腰直角三角形,
则∠ACO+∠BCO=∠ACO+∠DCO=∠ACD=45°.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案【题目】某学校一班级开展为贫困山区学生捐钱助学活动,该班有20名学生捐出了自己的零花钱,捐款数如下:(单位:元)
19 | 20 | 25 | 30 | 28 | 27 | 26 | 21 | 20 | 22 | 24 | 23 | 25 | 29 | 27 | 28 | 27 | 30 | 19 | 20 |
该班老师准备将此次活动的捐款数据制成频数分布直方图,在制图时请你帮老师算出以下数据:
(1)计算最大值与最小值的差;
(2)若选定组距为2计算将这20个数据分成的组数;并计算将第一组的起点定为18.5时捐款数在26.5-28.5范围内的频数;
(3)计算第一组和最后一组这两个组内包含的所有样本的平均数