��Ŀ����
����Ŀ��ijУ��֯ѧ������ؽ������ʵ���������680��ѧ���μӣ���Я��300�����ѧУ�ƻ����üס��������ͺŵ�������20�������˽⣬��������ÿ���������40�˺�10�������������ÿ���������30�˺�20�����
��1����ΰ��żס�������������һ���Եؽ�ѧ��������ȫ�����ߣ����ļ��ַ�����
��2������ס�����������ÿ��������÷ֱ�Ϊ2000Ԫ��1800Ԫ������ѡ����ʡǮ��һ���������
���𰸡������ü�������8������������12���������ü�������9������������11����
�����ü�������10������������10������2����ʡǮ��������ǣ����ü�������8������������12����
�������������������1�����ȸ��������г�����ʽ���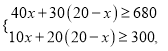
���![]() ��ȡֵ��Χ�����ȷ��
��ȡֵ��Χ�����ȷ��![]() ��ȡֵ������ȷ�������巽����
��ȡֵ������ȷ�������巽����
��2���������������ܷ���![]() �ĺ�����ϵʽ���ٸ���һ�κ�����������ȷ���ܷ�����С���������
�ĺ�����ϵʽ���ٸ���һ�κ�����������ȷ���ܷ�����С���������
�����������1���谲��![]() ����������������
����������������![]() ������������
������������
�������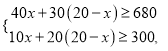 ����ã�
����ã� ![]()
������![]() ��ȡ8��9��10��
��ȡ8��9��10��
������ַ�����
�����ü�������8������������12����
�����ü�������9������������11����
�����ü�������10������������10����
��2��������ַ�����
�����ü�������8������������12����
�����ü�������9������������11����
�����ü�������10������������10����
��2������ܷ���Ϊ![]() Ԫ����
Ԫ����![]()
��![]() ��
��![]() �����������
�����������
�൱![]() ʱ��
ʱ�� ![]() ��С=200��8+36000=37600��
��С=200��8+36000=37600��
����ʡǮ��������ǣ����ü�������8������������12����