题目内容
【题目】新定义:我们把两个面积相等但不全等的三角形叫做偏等积三角形.
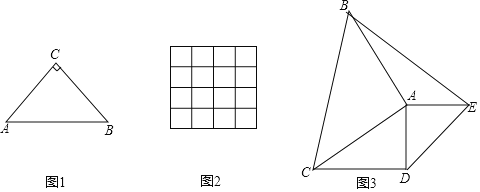
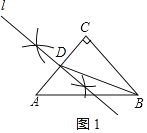
(1)初步尝试:如图1,已知等腰直角△ABC,∠ACB=90°,请用直尺和圆规将它分成两个三角形,使它们成为偏等积三角形,请保留作图痕迹.
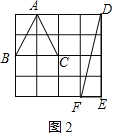
(2)理解运用:请在图2的方格纸中,画两个面积为2的三角形,使这两个三角形是偏等积三角形.
(3)综合应用:如图3,已知△ACD为直角三角形,∠ADC=90°,以AC,AD为腰向外作等腰直角三角形ABC和等腰直角三角形ADE,∠CAB=∠DAE=90°,连结BE,求证:△ACD与△ABE为偏等积三角形.
【答案】(1)作图见解析;(2)作图见解析;(3)证明见解析.
【解析】
(1)尺规作图找出AC的中点D,连结BD,则△BAD和△BCD为偏等积三角形.
(2)利用“友好三角形”的定义得出,△ABC与△DEF为“友好三角形”.
(3)过点B作BH⊥AE,垂足为H,先证明△ABH≌△ACD,则CD=HB.,依据三角形的面积公式可知S△ABE=S△CDA,然后再依据偏等积三角形的定义进行证明即可.
(1)如图1所示,△ABD和△BCD是偏等积三角形;
(2)如图2所示,△ABC和△DEF是偏等积三角形;
(3)如图3所示:过点B作BH⊥AE,垂足为H.
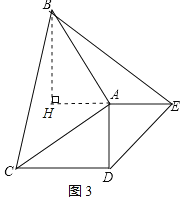
∵等腰直角三角形ABC和等腰直角三角形ADE,∠CAB=∠DAE=90°,
∴∠HAC+∠DAC=90°,∠BAH+∠HAC=90°.
∴∠BAH=∠DAC.
在△ABH和△ACD中
∵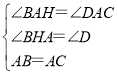 ,
,
∴△ABH≌△ACD(AAS),
∴BH=CD,
∵S△ABE=![]() BHAE,S△ACD=
BHAE,S△ACD=![]() ADCD,
ADCD,
∵AE=AD,CD=BH,
∴S△ABE=S△ACD,
又由图知,这两个三角形不全等,
∴△ACD与△ABE为偏等积三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目