题目内容
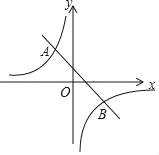
【题目】如图，已知A(m，2)，B(2，n)是一次函数y＝﹣x+1的图象与反比例函数y＝
(k≠0)图象的两个交点．
(1)求反比例函数的解析式；
(2)根据图象，请直接写出关于x的不等式﹣x+1＜的解集．
【答案】(1)反比例函数的表达式为y＝﹣
；(2)当﹣x+1＜
时，﹣1＜x＜0或x＞2．
【解析】
（1）把点A的坐标代入一次函数解析式求得m的值，然后将点A的坐标代入反比例函数解析式求得k的值即可；
（2）根据函数图象可以直接得到答案．
(1)∵A(m，2)在一次函数y＝﹣x+1的图象上，
∴m＝﹣1．
∴A(﹣1，2)．
∵A(﹣1，2)在反比例函数y＝
(k≠0)的图象上，
∴k＝﹣2．
∴反比例函数的表达式为y＝﹣
．
(2)由图象知，当﹣x+1＜时，﹣1＜x＜0或x＞2．
练习册系列答案
相关题目
【题目】未成年人思想道德建设越来越受到社会的关注，辽阳青少年研究所随机调查了本市一中学100名学生寒假中花零花钱的数量(钱数取整数元)，以便引导学生树立正确的消费观．根据调查数据制成了频
分组 | 频数 | 频率 |
0.5～50.5 |
| 0.1 |
50.5～ | 20 | 0.2 |
100.5～150.5 |
|
|
200.5 | 30 | 0.3 |
200.5～250.5 | 10 | 0.1 |
率分布表和频率分布直方图(如图)．
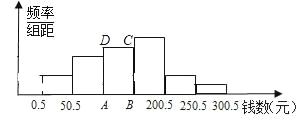
(1)补全频率分布表；
(2)在频率分布直方图中，长方形ABCD的面积是 ；这次调查的样本容量是 ；
(3)研究所认为，应对消费150元以上的学生提出勤俭节约的建议．试估计应对该校1000名学生中约多少名学生提出这项建议．
