Question

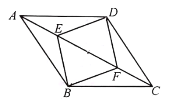
【题目】如图，E,F是菱形ABCD对角线上的两点，且AE=CF.

（1）求证：四边形BEDF是菱形；

（2）若，AD=6，AE=DE，求菱形BEDF的周长

Answer 1

【答案】（1）详见解析；（2）

【解析】

（1）连接BD，由菱形ABCD的性质得出OA=OC，OB=OD，AC⊥BD，得出OE=OF，证出四边形BEDF是平行四边形，再由EF⊥BD，即可证出四边形BEDF是菱形；
（2）求出∠DAE=30°，得出再证出∠ADE=∠EDO=30°，在Rt△DEO中，由三角函数求出 即可得出菱形BEDF的周长．

(1)证明：连接BD，交AC于O，如图所示：

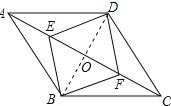
∵四边形ABCD是菱形，

∴OA=OC，OB=OD，AC⊥BD，

∵AE=CF，

∴OE=OF，

∴四边形BEDF是平行四边形，

∵EF⊥BD，

∴四边形BEDF是菱形；

(2)∵

∴

∵AD=6，

∴

∵AE=DE，

∴

在Rt△DEO中,

∴菱形BEDF的周长