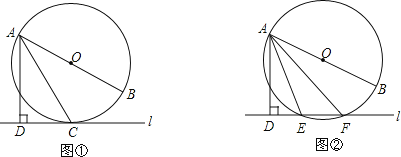题目内容
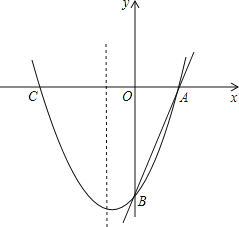
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,﹣3),点P是直线BC下方抛物线上的任意一点.
(1)求这个二次函数y=x2+bx+c的解析式.
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形POP′C,如果四边形POP′C为菱形,求点P的坐标.
(3)如果点P在运动过程中,能使得以P、C、B为顶点的三角形与△AOC相似,请求出此时点P的坐标.

【答案】(1)y=x2﹣2x﹣3(2)(2)(![]() ,-
,-![]() )(3)P、C、B为顶点的三角形与△AOC相似,此时点P的坐标(1,﹣4)
)(3)P、C、B为顶点的三角形与△AOC相似,此时点P的坐标(1,﹣4)
【解析】
(1)根据待定系数法,可得函数解析式;
(2)根据菱形的对角线互相垂直平分,可得P点的纵坐标,根据自变量与函数值的对应关系,可得答案;
(3)分类讨论:①当∠PCB=90°,根据互相垂直的两条直线的一次项系数互为负倒数,可得BP的解析式,根据自变量与函数值的对应关系,可得P点坐标;根据勾股定理,可得BC,CP的长,根据两组对边对应成比例且夹角相等的两个三角形相似,可得答案;
②当∠BPC=90°时,根据相似三角形的性质,可得P点的坐标,根据两组对边对应成比例且夹角相等的两个三角形相似,可得答案.
(1)将B、C点代入函数解析式,得:![]() ,解得:
,解得:![]() ,这个二次函数y=x2+bx+c的解析式为y=x2﹣2x﹣3;
,这个二次函数y=x2+bx+c的解析式为y=x2﹣2x﹣3;
(2)∵四边形POP′C为菱形,∴OC与PP′互相垂直平分,∴yP![]() ,即x2﹣2x﹣3
,即x2﹣2x﹣3![]() ,解得:x1
,解得:x1![]() ,x2
,x2![]() (舍),P(
(舍),P(![]() );
);
(3)∵∠PBC<90°,∴分两种情况讨论:
①如图1,当∠PCB=90°时,过P作PH⊥y轴于点H,BC的解析式为y=x﹣3,CP的解析式为y=﹣x﹣3,设点P的坐标为(m,﹣3﹣m),将点P代入代入y═x2﹣2x﹣3中,解得:m1=0(舍),m2=1,即P(1,﹣4);
AO=1,OC=3,CB![]() ,CP
,CP![]() ,此时
,此时![]() 3,△AOC∽△PCB;
3,△AOC∽△PCB;
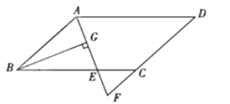
②如图2,当∠BPC=90°时,作PH⊥y轴于H,作BD⊥PH于D.
∵PC⊥PB,∴△PHC∽△BDP,∴![]() .设点P的坐标为(m,m2﹣2m﹣3),则PH=m,HC=-(m2﹣2m﹣3)-(-3)=-m2+2m,BD=-(m2﹣2m﹣3),PD=3-m,∴
.设点P的坐标为(m,m2﹣2m﹣3),则PH=m,HC=-(m2﹣2m﹣3)-(-3)=-m2+2m,BD=-(m2﹣2m﹣3),PD=3-m,∴![]() ,∴
,∴![]() ,解得:m
,解得:m![]() 或
或![]() (舍去).当m
(舍去).当m![]() 时,m2﹣2m﹣3=
时,m2﹣2m﹣3=![]() .
.
∵△PHC∽△BDP,∴![]() =
=![]() =
=![]()
![]() 3,以P、C、B为顶点的三角形与△AOC不相似.
3,以P、C、B为顶点的三角形与△AOC不相似.
综上所述:P、C、B为顶点的三角形与△AOC相似,此时点P的坐标(1,﹣4).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某通信公司策划了![]() 两种上网的月收费方式:
两种上网的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/ | 超时费/(元/ |
| 30 | 25 | 0.05 |
|
|
|
|
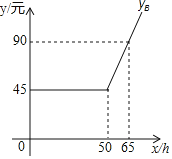
设每月上网时间为![]() ,方式
,方式![]() 的收费金额分别为
的收费金额分别为![]() (元),
(元),![]() (元),如图是
(元),如图是![]() 与
与![]() 之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
(1)![]() ,
,![]() ,
,![]() ;
;
(2)求![]() 之间的函数解析式;
之间的函数解析式;
(3)若每月上网时间为31小时,请直接写出选择哪种方式能节省上网费.