题目内容
【题目】如图，已知直线y=3x﹣3分别交x轴、y轴于A、B两点，抛物线y=x2+bx+c经过A、B两点，点C是抛物线与x轴的另一个交点（与A点不重合）．
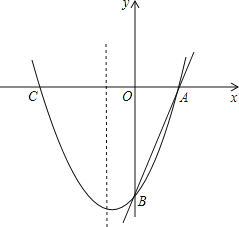
（1）求抛物线的解析式；
（2）求△ABC的面积；
（3）在抛物线的对称轴上，是否存在点M，使△ABM为等腰三角形？若不存在，请说明理由；若存在，求出点M的坐标．
【答案】解：（1）∵直线y=3x﹣3分别交x轴、y轴于A、B两点，
∴可得A（1，0），B（0，﹣3），
把A、B两点的坐标分别代入y=x2+bx+c得：
，解得：
。
∴抛物线解析式为：y=x2+2x﹣3。
（2）令y=0得：0=x2+2x﹣3，解得：x1=1，x2=﹣3。
∴C点坐标为：（﹣3，0），AC=4，
∴S△ABC=
AC×OB=
×4×3=6。
（3）存在。
易得抛物线的对称轴为：x=﹣1，假设存在M（﹣1，m）满足题意，
根据勾股定理，得
。
分三种情况讨论：
①当AM=AB时，
，解得：
。
∴M1（﹣1，
），M2（﹣1，
）。
②当BM=AB时，
，解得：M3=0，M4=﹣6。
∴M3（﹣1，0），M4（﹣1，﹣6）。
③当AM=BM时，
，解得：m=﹣1。
∴M5（﹣1，﹣1）。
综上所述，共存在五个点使△ABM为等腰三角形，坐标为M1（﹣1，
），M2（﹣1，
），M3（﹣1，0），M4（﹣1，﹣6），M5（﹣1，﹣1）。
【解析】
试题（1）根据直线解析式求出点A及点B的坐标，然后将点A及点B的坐标代入抛物线解析式，可得出b、c的值，求出抛物线解析式。
（2）由（1）求得的抛物线解析式，可求出点C的坐标，继而求出AC的长度，代入三角形的面积公式即可计算。
（3）根据点M在抛物线对称轴上，可设点M的坐标为（﹣1，m），分三种情况讨论，①AM=AB，②BM=AB，③AM=BM，求出m的值后即可得出答案。
【题目】某数学学习网站为吸引更多人注册加入，举行了一个为期5天的推广活动，在活动期间，加入该网站的人数变化情况如下表所示：
时间 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
新加入人数（人） | 153 | 550 | 653 | b | 725 |
累计总人数（人） | 3353 | 3903 | a | 5156 | 5881 |
（1）表格中a= ，b= ；
（2）请把下面的条形统计图补充完整；
（3）根据以上信息，下列说法正确的是 （只要填写正确说法前的序号）．
①在活动之前，该网站已有3200人加入；
②在活动期间，每天新加入人数逐天递增；
③在活动期间，该网站新加入的总人数为2528人．
