题目内容
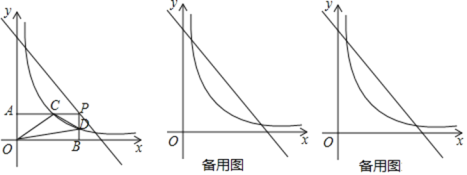
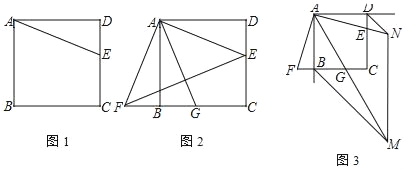
【题目】综合与探究:如图,在平面直角坐标系中,Rt△AOC的直角边OC在y轴正半轴上,且顶点O与坐标原点重合,点A的坐标为(2,4),直线y=-x+b过点A,与x轴交于点B.
(1)求点B的坐标及直线AB的解析式;
(2)动点P从点O出发,以每秒1个单位长的速度,沿O-C-A的路线向点A运动,同时动点M从点B出发,以相同的速度沿BO的方向向O运动,过点M作MQ⊥x轴,交线段BA或线段AO于点Q,当点P到达A点时,点P和点M都停止运动.在运动过程中,设动点P运动的时间为t秒.△APQ的面积为S,求S关于t的函数关系式;
(3)是否存在以M、P、Q为顶点的三角形的面积与S相等?若存在,求t的值;若不存在,请说明理由.
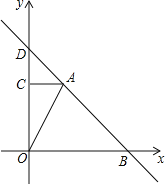
【答案】(1)点B的坐标为(6,0);直线AB的解析式为:y=-x+6;(2)S= ;(3)t=2或
;(3)t=2或![]() .
.
【解析】
(1)先将点A(2,4)代入y=-x+b,运用待定系数法求出直线AB的解析式,再令y=0,求出x的值,即可得到与x轴交点B的坐标;
(2)①先求出直线AB与y轴交点D的坐标,由B、D两点的坐标,可知△OBD是等腰直角三角形,再过点A作AN⊥OB于N,可得AN=OC=4,BN=AN=4,则当点P到达点C时,点M到达点N,所以分两种情况讨论:(i)当0≤t≤4,即点P在OC上,点Q在BA上时,用含t的代数式分别表示PQ、CP,再根据S=![]() PQCP即可求解;(ii)当4<t≤6,即点P在AC上,点Q在AO上时,延长MQ交AC于点E,用含t的代数式分别表示AP、QE,再根据S=
PQCP即可求解;(ii)当4<t≤6,即点P在AC上,点Q在AO上时,延长MQ交AC于点E,用含t的代数式分别表示AP、QE,再根据S=![]() APQE即可求解;
APQE即可求解;
②分两种情况讨论:(i)当0≤t≤4,即点P在OC上,点Q在BA上时,先由三角形面积公式求出S△MPQ=-![]() t2+3t,再根据S△MPQ=S=
t2+3t,再根据S△MPQ=S=![]() t2-5t+12列出方程,解方程即可;(ii)当4<t≤6,即点P在AC上,点Q在AO上时,先由三角形面积公式求出S△MPQ=(6-t)|10-2t|,再根据S△MPQ=S=(6-t)(t-4),列出方程,解方程即可.
t2-5t+12列出方程,解方程即可;(ii)当4<t≤6,即点P在AC上,点Q在AO上时,先由三角形面积公式求出S△MPQ=(6-t)|10-2t|,再根据S△MPQ=S=(6-t)(t-4),列出方程,解方程即可.
(1)将点A(2,4)代入y=-x+b,
得4=-2+b,解得b=6,
∴直线AB的解析式为:y=-x+6,
当y=0时,x=6,
∴点B的坐标为(6,0).
(2)设直线y=-x+6与y轴交于点D,则D(0,6),∵B(6,0),
∴OB=OD=6,∠OBD=∠ODB=45°.
过点A(2,4)作AN⊥OB于N,则AN=OC=4,ON=AC=2,BN=AN=4,

∴当点P到达点C时,点M到达点N.
分两种情况讨论:
(i)当0≤t≤4时,点P在OC上,点Q在BA上,如图1.
∵OP=t,BM=QM=t,
∴PQ∥OB,PQ=OM=OB-BM=6-t,CP=OC-OP=4-t,
∴S=![]() PQCP=
PQCP=![]() (6-t)(4-t)=
(6-t)(4-t)=![]() t2-5t+12;
t2-5t+12;
(ii)当4<t≤6时,点P在AC上,点Q在AO上,如图2,延长MQ交AC于点E.

∵OC+CP=t,BM=t,
∴AP=6-t,OM=OB-BM=6-t.
∵tan∠AON=![]() ,
,
∴![]() ,
,
∴QM=12-2t,
∴QE=EM-QM=4-(12-2t)=2t-8,
∴S=![]() APQE=
APQE=![]() (6-t)(2t-8)=-t2+10t-24.
(6-t)(2t-8)=-t2+10t-24.
综上可知,S= ;
;
②存在以M、P、Q为顶点的三角形的面积与S相等,理由如下:
分两种情况讨论:
(i)当0≤t≤4时,点P在OC上,点Q在BA上,如图3.
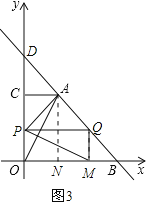
∵S△MPQ=![]() PQQM=
PQQM=![]() (6-t)t=-
(6-t)t=-![]() t2+3t,S=
t2+3t,S=![]() t2-5t+12,
t2-5t+12,
∴-![]() t2+3t=
t2+3t=![]() t2-5t+12,
t2-5t+12,
整理,得t2-8t+12=0,
解得t1=2,t2=6(不合题意舍去);
(ii)当4<t≤6时,点P在AC上,点Q在AO上,如图4.
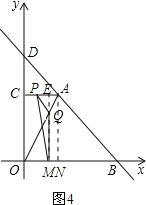
∵QM=12-2t,PE=|CE-CP|=|(6-t)-(t-4)|=|10-2t|,
∴S△MPQ=![]() QMPE=
QMPE=![]() (12-2t)|10-2t|=(6-t)|10-2t|,
(12-2t)|10-2t|=(6-t)|10-2t|,
又∵S=![]() APQE=
APQE=![]() (6-t)(2t-8)=(6-t)(t-4),
(6-t)(2t-8)=(6-t)(t-4),
∴(6-t)|10-2t|=(6-t)(t-4),
∵t=6时,M与Q重合,不合题意舍去,
∴10-2t=±(t-4),
当10-2t=t-4时,t=![]() ;
;
当10-2t=-(t-4)时,t=6舍去.
综上可知,存在以M、P、Q为顶点的三角形的面积与S相等,此时t的值为2或![]() .
.

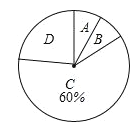
【题目】今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
评估成绩n(分) | 评定等级 | 频数 |
90≤n≤100 | A | 2 |
80≤n<90 | B | |
70≤n<80 | C | 15 |
n<70 | D | 6 |
根据以上信息解答下列问题:
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.