题目内容
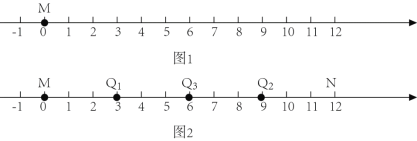
【题目】如图,在每个小正方形边长为1的方格纸中,每个小方格的顶点叫做格点.
(1)画出△ABC中AB边上的中线CD;
(2)画出△ABC向右平移3个单位长度后得到的△A1B1C1;
(3)图中AC与A1C1的关系是 ;
(4)在图中,能使S△ABQ=S△ABC的格点Q共有 个,分别用Q1、Q2、…表示出来.
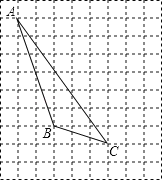
【答案】(1)见解析;(2)见解析;(3)平行且相等;(4)4.
【解析】
(1)根据中线的定义得出AB的中点即可得出△ABC的AB边上的中线CD;
(2)平移A,B,C各点,得出各对应点,连接得出△A1B1C1;
(3)利用平移的性质得出AC与A1C1的关系;
(4)首先求出S△ABC的面积,进而得出Q点的个数.
解:(1)AB边上的中线CD如图所示:
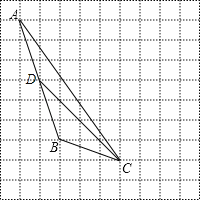 ;
;
(2)△A1B1C1如图所示:
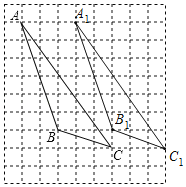 ;
;
(3)根据平移的性质得出,AC与A1C1的关系是:平行且相等;
故答案为:平行且相等;
(4)如图所示:能使S△ABQ=S△ABC的格点Q,共有4个.
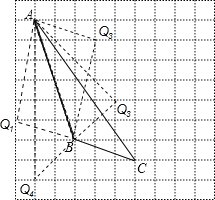
故答案为:4.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
【题目】某校八年级学生开展踢毽子比赛活动,每班选派5名学生参加,在规定时间内每人踢100个以上(含100个)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个),请根据表中数据解答下列问题:
1号 | 2号 | 3号 | 4号 | 5号 | 总分 | |
甲班 | 90 | 100 | 96 | 116 | 98 | 500 |
乙班 | 100 | 95 | 108 | 92 | 105 | 500 |
(1)计算甲、乙两班的优秀率;
(2)求出甲、乙两班比赛数据的中位数和方差;
(3)根据(1)(2)的计算结果,请你判定甲班与乙班的比赛名次.