题目内容
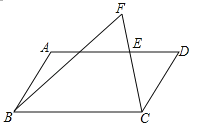
【题目】如图,在ABCD中,E是AD上一点,延长CE到点F,使∠FBC=∠DCE.
(1)求证:∠D=∠F;
(2)用直尺和圆规在AD上作出一点P,使△BPC∽△CDP(保留作图的痕迹,不写作法).
【答案】(1)证明见解析;(2)答案见解析.
【解析】
(1)BE交AD于G,先利用AD∥BC得到∠FBC=∠FGE,加上∠FBC=∠DCE,所以∠FGE=∠DCE,然后根据三角形内角和定理易得∠D=∠F;
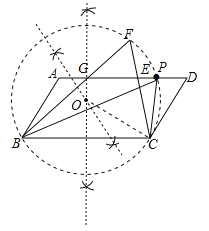
(2)分别作BC和BF的垂直平分线,它们相交于点O,然后以O为圆心,OC为半径作△BCF的外接圆⊙O,⊙O交AD于P,连结BP、CP,则根据圆周角定理得到∠F=∠BPC,而∠F=∠D,所以∠D=∠BPC,接着可证明∠PCD=∠APB=∠PBC,于是可判断△BPC∽△CDP.
解:(1)BE交AD于G.如图,∵四边形ABCD为平行四边形,∴AD∥BC,∴∠FBC=∠FGE.
而∠FBC=∠DCE,∴∠FGE=∠DCE.
∵∠GEF=∠DEC,∴∠D=∠F;
(2)如图,点P为所作.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了解某区八年级学生的睡眠情况,随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人,利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表(单位:小时)
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
二、学生睡眠情况统计图
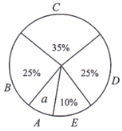
根据图表提供的信息,回答下列问题:
(1)试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数;
(2)如果睡眠时间x(时)满足:![]() ,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
(3)如果将各组别学生睡眠情况分组的最小值(如C组别中,取![]() ),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.