题目内容
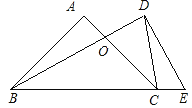
【题目】如图,在平面内,菱形 ABCD 的对角线相交于点 O,点 O 又是菱形B1A1OC1的一个顶点,菱形 ABCD≌菱形 B1A1OC1,AB=BD=10.菱形B1A1OC1 绕点 O 转动,求两个菱形重叠部分面积的取值范围,请说明理由.

【答案】![]() ≤s
≤s ![]() .
.
【解析】
分别求出重叠部分面积的最大值,最小值即可解决问题
如图1中,∵四边形ABCD是菱形,
∴AB=AD,∵AB=BD,
∴AB=BD=AD=10,
∴△ABD是等边三角形,
当AE=EB,AF=FD时,重叠部分的面积最大,最大面积=![]() S△ABD=
S△ABD=![]() ×
×![]() ×102=
×102=![]() ,
,
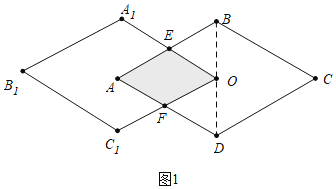
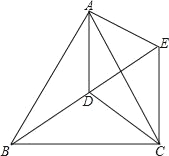
如图2中,当OA1与BC交于点E,OC1交AB与F时,作OG⊥AB与G,OH⊥BC于H.
易证△OGF≌△OHE,

∴S四边形BEOF=S四边形OGBH=![]() ×
×![]() =
=![]() ,
,
观察图象图象可知,在旋转过程中,重叠部分是三角形时,当点E与B重合,此时三角形的面积最小为![]() ,
,
综上所述,重叠部分的面积S的范围为![]() ≤s≤
≤s≤![]() .
.

练习册系列答案
相关题目