题目内容
【题目】如图①,矩形ABCD被对角线AC分为两个直角三角形,AB=3,BC=6.现将Rt△ADC绕点C顺时针旋转90°,点A旋转后的位置为点E,点D旋转后的位置为点F.以C为原点,以BC所在直线为x轴,以过点C垂直于BC的直线为y轴,建立如图②的平面直角坐标系.

(1)求直线AE的解析式;
(2)将Rt△EFC沿x轴的负半轴平行移动,如图③.设OC=x(0<x≤9),Rt△EFC与Rt△ABO的重叠部分面积为s;求当x=1与x=8时,s的值;
(3)在(2)的条件下s是否存在最大值?若存在,求出这个最大值及此时x的值;若不存在,请说明理由.
【答案】(1)直线AE解析式为:![]() ;(2) ①
;(2) ①![]() ;②
;②![]() ;(3) 当
;(3) 当![]() 时,存在S的最大值,S最大=
时,存在S的最大值,S最大=![]() .
.
【解析】
试题
(1)由题意易得点A、E的坐标分别为(-6,3)和(3,6),由此设直线AE的解析式为y=kx+b,代入A、E的坐标列出方程组,求得k、b的值即可得到所求解析式;
(2)①如图1,当x=1时,重叠部分为△POC,由此时△POC∽△BOA,结合S△BOA=![]() AB·BO即可求得重叠部分的面积;②如图2,当x=8时,重叠部分是梯形ABFQ,由已知条件计算可得:AB=3、BF=1、FQ=2.5,从而可由梯形面积公式计算出重叠部分的面积;
AB·BO即可求得重叠部分的面积;②如图2,当x=8时,重叠部分是梯形ABFQ,由已知条件计算可得:AB=3、BF=1、FQ=2.5,从而可由梯形面积公式计算出重叠部分的面积;
(3)由画图分析可知,当0<x≤3与7.5<x≤9时,不会出现s的最大值;而当3<x≤6时,由图3可知:当x=6时,s最大;当6<x≤7.5时,如图4,此时也存在一个区间的最大值,结合图形和已知条件分别求出当3<x≤6时和6<x≤7.5时重叠部分面积的最大值,并进行比较,即可得到移动过程中s的最大值及对应的x的值.
试题解析:
(1)AB=3,BC=6,根据旋转的性质可知:A(﹣6,3),E(3,6),
设函数解析式为y=kx+b,
把A(﹣6,3),E(3,6)分别代入解析式得,![]() ,解得:
,解得: .
.
∴直线AE解析式为:![]() .
.
(2)①当x=1时,如图1,重叠部分为△POC,
可得:Rt△POC∽Rt△BOA,
∴![]() ,由已知条件计算可得:
,由已知条件计算可得:![]() ,解得:
,解得:![]() .
.
②当x=8时,如图2,重叠部分为梯形FQAB,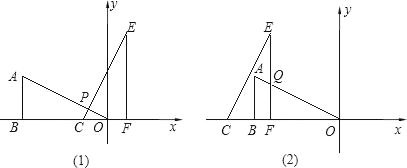
由已知条件计算可得:OF=5,BF=1,FQ=2.5,
∴S=![]() (FQ+AB)·BF=
(FQ+AB)·BF=![]() (2.5+3)×1=
(2.5+3)×1=![]() .
.
(3)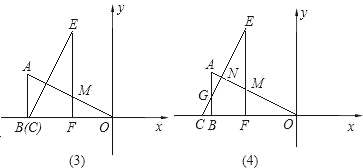
①显然,画图分析,从图中可以看出:当0<x≤3与7.5<x≤9时,不会出现s的最大值.
②当3<x≤6时,由图3可知:当x=6时,s最大.
此时,由已知条件计算可得:S△OBN=![]() ,S△OMF=
,S△OMF=![]() ,
,
∴S= S△OBN- S△OMF=![]() .
.
③当6<x≤7.5时,如图4,由已知条件计算可得:S△OCN=![]() ,S△OFM=
,S△OFM=![]() ,S△BCG=
,S△BCG=![]() .
.
∴S=S△OCN﹣S△OFM﹣S△BCG=![]() ,
,
∴S=![]() ,
,
∴当![]() 时,S有最大值,S最大=
时,S有最大值,S最大=![]() ,
,
综合得:当![]() 时,存在S的最大值,S最大=
时,存在S的最大值,S最大=![]() .
.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案【题目】某中学为了解某年级1200名学生每学期参加社会实践活动时间,随机对该年级50名学生进行了调查,结果如下表:
时间(天) | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
人 数 | 1 | 2 | 4 | 5 | 7 | 11 | 8 | 6 | 4 | 2 |
(1)在这个统计中,众数是 ,中位数是 ;
(2)补全下面的频率分布表和频率分布直方图:
分组 | 频数 | 频率 |
3.5~5.5 | 3 | 0.06 |
5.5~7.5 | 9 | 0.18 |
7.5~9.5 | 0.36 | |
9.5~11.5 | 14 | |
11.5~13.5 | 6 | 0.12 |
合 计 | 50 | 1.00 |

(3)请你估算这所学校该年级的学生中,每学期参加社会实践活动时间不少于9天的大约有多少人?