题目内容
已知△ABC和△A′B′C′中,AB=A′B′,AC=A′C′,∠A=∠A′=50°,∠C′=48°,则∠B=
82°
82°
度.分析:根据SAS证△ABC≌△A′B′C′,推出∠C=∠C′=48°,在△ABC中,根据三角形的内角和定理求出即可.
解答: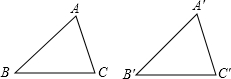
解:∵在△ABC和△A′B′C′中
∴△ABC≌△A′B′C′(SAS),
∴∠C=∠C′=48°,
∵∠A=50°,
∴∠B=180°-∠A-∠C=82°,
故答案为:82.

解:∵在△ABC和△A′B′C′中
|
∴△ABC≌△A′B′C′(SAS),
∴∠C=∠C′=48°,
∵∠A=50°,
∴∠B=180°-∠A-∠C=82°,
故答案为:82.
点评:本题考查了全等三角形的性质和判定,注意:全等三角形的对应角相等,对应边相等,全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
相关题目
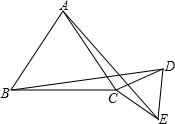 如图,已知△ABC和△CDE都是等边三角形,问:线段AE、BD的长度有什么关系?请说明理由.
如图,已知△ABC和△CDE都是等边三角形,问:线段AE、BD的长度有什么关系?请说明理由.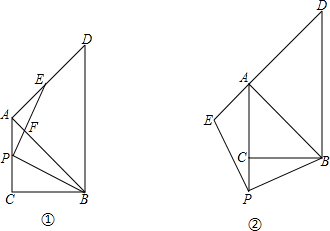
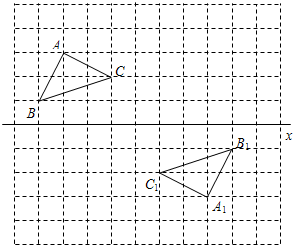 如图,在正方形网格中每个小正方形的边长都是单位1,已知△ABC和△A1B1C1关于点O成中心对称,点O直线x上.
如图,在正方形网格中每个小正方形的边长都是单位1,已知△ABC和△A1B1C1关于点O成中心对称,点O直线x上. 30、如图,已知△ABC和点O.
30、如图,已知△ABC和点O.