题目内容
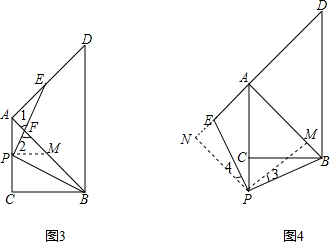
如图,已知△ABC和△ABD均为等腰直角三角形,∠ACB=∠BAD=90°,点P为边AC上任意一点(点P不与A、C两点重合),作PE⊥PB交AD于点E,交AB于点F.
(1)求证:∠AEP=∠ABP.
(2)猜想线段PB、PE的数量关系,并证明你的猜想.
(3)若P为AC延长线上任意一点(如图②),PE交DA的延长线于点E,其他条件不变,(2)中的结论是否成立?请证明你的结论.

(1)求证:∠AEP=∠ABP.
(2)猜想线段PB、PE的数量关系,并证明你的猜想.
(3)若P为AC延长线上任意一点(如图②),PE交DA的延长线于点E,其他条件不变,(2)中的结论是否成立?请证明你的结论.

分析:(1)根据题意可得∠EPB=∠BAD=90°,再由∠AEP=90°-∠1,∠ABP=90°-∠2,∠1=∠2可得∠AEP=∠ABP;
(2)过P作PM⊥AC交AB与M,证明△APE≌△MPB可得PB=PE;
(3)过P作PM⊥AB于点M,作PN⊥DA交DA延长线于点N,证明△PBM≌△PEN,可得PB=PE.
(2)过P作PM⊥AC交AB与M,证明△APE≌△MPB可得PB=PE;
(3)过P作PM⊥AB于点M,作PN⊥DA交DA延长线于点N,证明△PBM≌△PEN,可得PB=PE.
解答:证明:(1)∵PE⊥PB,
∴∠EPB=90°,
∵∠BAD=90°,
∴∠AEP=90°-∠1,∠ABP=90°-∠2,
∵∠1=∠2,
∴∠AEP=∠ABP;
(2)PB=PE,
如图3,过P作PM⊥AC交AB与M,
在等腰直角三角形ABC中,∠BAC=45°,
∴∠PAM=∠AMP=45°,
∴PA=PM,
∵∠PAE=45°+90°=135°,∠PMB=180°-45°=135°,
∴∠PAE=∠PMB,
在△AEP和△MBP中
,
∴△APE≌△MPB(AAS),
∴PB=PE;
(3)成立;
如图4,过P作PM⊥AB于点M,作PN⊥DA交DA延长线于点N,
∵∠PAB=∠PAN=45°,
∴PM=PN,
∵∠3+∠MPE=∠4+∠MPE=90°,
∴∠3=∠4,
∵∠PMB=∠N=90°,
在△PBM和△PEN中
,
∴△PBM≌△PEN(ASA),
∴PB=PE.
∴∠EPB=90°,
∵∠BAD=90°,
∴∠AEP=90°-∠1,∠ABP=90°-∠2,
∵∠1=∠2,
∴∠AEP=∠ABP;
(2)PB=PE,
如图3,过P作PM⊥AC交AB与M,
在等腰直角三角形ABC中,∠BAC=45°,
∴∠PAM=∠AMP=45°,
∴PA=PM,
∵∠PAE=45°+90°=135°,∠PMB=180°-45°=135°,
∴∠PAE=∠PMB,
在△AEP和△MBP中
|

∴△APE≌△MPB(AAS),
∴PB=PE;
(3)成立;
如图4,过P作PM⊥AB于点M,作PN⊥DA交DA延长线于点N,
∵∠PAB=∠PAN=45°,
∴PM=PN,
∵∠3+∠MPE=∠4+∠MPE=90°,
∴∠3=∠4,
∵∠PMB=∠N=90°,
在△PBM和△PEN中
|
∴△PBM≌△PEN(ASA),
∴PB=PE.
点评:此题主要考查了全等三角形的判定与性质,关键是掌握全等三角形的判定定理与性质定理.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目

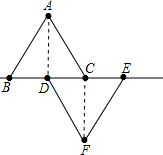 ,连接AD、CF.
,连接AD、CF.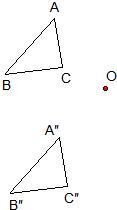 19、如图,已知△ABC和△A″B″C″及点O.
19、如图,已知△ABC和△A″B″C″及点O. 23、如图,已知△ABC和两条相交于O点且夹角为60°的直线m、n.
23、如图,已知△ABC和两条相交于O点且夹角为60°的直线m、n.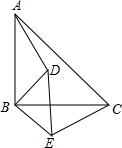 (2012•南岗区二模)如图,已知△ABC和△DBE均为等腰直角三角形,∠ABC=∠DBE=90°,求证:AD=CE.
(2012•南岗区二模)如图,已知△ABC和△DBE均为等腰直角三角形,∠ABC=∠DBE=90°,求证:AD=CE.