题目内容
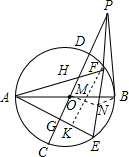
设AB,CD为圆O的两直径,过B作PB垂直AB,并与CD延长线相交于点P,过P作直线PE,与圆分别交于E,F两点,连AE,AF分别与CD交于G,H两点(如图),求证:OG=OH.


证明:过点F作FK∥GH交OB于M,交AE于K,过O点作ON⊥EF于N,如图,
∵PB⊥OB,
∴∠ONP=∠OBP=90°,
∴点O,P,B,N四点共圆,
∴∠OPN=∠OBN,
而FK∥GH,
∴∠MFN=∠OPN,
∴∠MFN=∠OBN,
∴点M,F,B,N四点共圆,
∴∠MNF=∠MBF,
而∠MBF=∠E,
∴∠MNF=∠E,
∴MN∥KE,
又∵ON⊥EF,
∴NF=NE,
∴MF=MK,
而FK∥HG,
∴
=
,
=
,
∴
=
,
∴OG=OH.
∵PB⊥OB,
∴∠ONP=∠OBP=90°,
∴点O,P,B,N四点共圆,
∴∠OPN=∠OBN,
而FK∥GH,
∴∠MFN=∠OPN,
∴∠MFN=∠OBN,
∴点M,F,B,N四点共圆,
∴∠MNF=∠MBF,
而∠MBF=∠E,
∴∠MNF=∠E,
∴MN∥KE,
又∵ON⊥EF,
∴NF=NE,
∴MF=MK,
而FK∥HG,
∴
| OH |
| MF |
| OA |
| AM |
| OG |
| MK |
| OA |
| AM |
∴
| OH |
| MF |
| OG |
| MK |
∴OG=OH.


练习册系列答案
相关题目

 相交于点F、G.
相交于点F、G.
