题目内容
【题目】如图,BC是⊙O的直径,A是弦BD延长线上一点,切线DE平分AC于E。
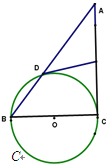
(1)求证:AC是⊙O的切线;
(2)若AD:DB=3:2,AC=15,求⊙O的直径。
【答案】(1)连接OD、CD,先根据切线的性质得到OD⊥DE,即∠1+∠2=90°,再根据圆周角定理可得∠BDC=90°,再结合E为AC的中点,根据直角三角形的性质可得DE=CE=AE=![]() AC,即得∠2=∠3,根据元的基本性质可得∠1=∠4,即得∠3+∠4=∠1+∠2=90°,从而证得结论;(2)
AC,即得∠2=∠3,根据元的基本性质可得∠1=∠4,即得∠3+∠4=∠1+∠2=90°,从而证得结论;(2)![]()
【解析】
试题分析:(1)连接OD、CD,先根据切线的性质得到OD⊥DE,即∠1+∠2=90°,再根据圆周角定理可得∠BDC=90°,再结合E为AC的中点,根据直角三角形的性质可得DE=CE=AE=![]() AC,即得∠2=∠3,根据元的基本性质可得∠1=∠4,即得∠3+∠4=∠1+∠2=90°,从而证得结论;
AC,即得∠2=∠3,根据元的基本性质可得∠1=∠4,即得∠3+∠4=∠1+∠2=90°,从而证得结论;
(2)分别证得△ACD∽△ABC与△ACD∽△BCD,根据相似三角形的性质可得![]() ,
,![]() ,由AD:DB=3:2可设AD=3k,DB=2k,则AB=5k,即可求得结果.
,由AD:DB=3:2可设AD=3k,DB=2k,则AB=5k,即可求得结果.
(1)连接OD、CD
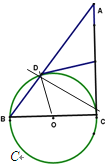
∵DE是⊙O的切线,切点为D
∴OD⊥DE于D
∴∠ODE=90°,即∠1+∠2=90°;
∵BC为⊙O的直径
∴∠BDC=90°
∴∠ADC=90°
∵E为AC的中点
∴DE=CE=AE=![]() AC
AC
∴∠2=∠3
∵⊙O中,OC=OD
∴∠1=∠4
∴∠3+∠4=∠1+∠2=90°
∴OC⊥AC于C
∴AC是⊙O的切线;
(2)∵∠ACD=∠BDC=90°,∠A=∠A
∴△ACD∽△ABC
同理:△ACD∽△BCD
∴![]() ①
①
![]() ②
②
∵AD:DB=3:2
∴设AD=3k,DB=2k,则AB=5k
∴①![]()
![]()
![]()
②![]()
![]()
∴![]() .
.

【题目】某厂从2011年起开始投入技改资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表所示:
年度 | 2011 | 2012 | 2013 | 2014 |
投入技改资金 | 2.5 | 3 | 4 | 4.5 |
产品成本 | 7.2 | 6 | 4.5 | 4 |
(1)请认真分析表中的数据,从你学过的一次函数和反比例函数中确定哪种函数能表示其变化规律,并求出它的表达式;
(2)按照这种变化规律,2015年已投入技改资金5万元.
①预计产品成本每件比2014年降低多少万元?
②如果打算在2015年把每件产品的成本降低到3.2万元,那么还需投入技改资金多少万元?(精确到0.01万元)
【题目】某公司有A、B两种型号的客车,它们的载客量、每天的租金如表所示:
A型号客车 | B型号客车 | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 600 | 450 |
已知某中学计划租用A、B两种型号的客车共10辆,同时送七年级师生到沙家参加社会实践活动,已知该中学租车的总费用不超过5600元.
(1)求最多能租用多少辆A型号客车?
(2)若七年级的师生共有380人,请写出所有可能的租车方案.