��Ŀ����
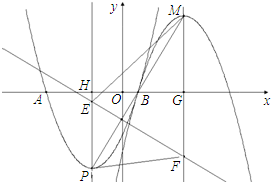
��2010•��ɽ��һģ����֪������C1��y=ax2+4ax+4a-5�Ķ���ΪP����x���ཻ��A��B���㣨��A�ڵ�B����ߣ�����B�ĺ�������1��
��1���������ߵĽ���ʽ�Ͷ���P�����ꣻ
��2������������x�ᷭ�ۣ�������ƽ�ƣ�ƽ�ƺ��������C2�Ķ���ΪM������P��M���ڵ�B�����ĶԳ�ʱ����ƽ�ƺ��������C2�Ľ���ʽ��
��3��ֱ��y=-
x+m��������C1��C2�ĶԳ���ֱ��ڵ�E��F�����ɵ�E��P��F��M���ɵ��ı��ε����Ϊs�����ú�m�Ĵ���ʽ��ʾs��
��1���������ߵĽ���ʽ�Ͷ���P�����ꣻ
��2������������x�ᷭ�ۣ�������ƽ�ƣ�ƽ�ƺ��������C2�Ķ���ΪM������P��M���ڵ�B�����ĶԳ�ʱ����ƽ�ƺ��������C2�Ľ���ʽ��
��3��ֱ��y=-
| 3 | 5 |
��������1�����Ȱ�������C1�䷽���ɵõ��������꣬Ȼ���B�����굱Ȼ���м��㼴�����������C1�Ľ���ʽ��
��2������PM����PH��x����H����MG��x����G��Ȼ��֤����PBH�ա�MBG����������ȫ�������ε��������M�����꣬���Ϳ������������C2�Ľ���ʽ��
��3�����ȷֱ���m��ʾE��F��������꣬Ȼ�����ۣ�
�ٵ�E���������С��-5ʱ����m�Ĵ���ʽ�ֱ��ʾPE��MF��Ȼ��Ϳ����ú�m�Ĵ���ʽ��ʾs��
�ڵ�E������������-5��F���������С��5ʱ��Ҳ��m�Ĵ���ʽ�ֱ��ʾPE��MF��Ȼ��Ϳ����ú�m�Ĵ���ʽ��ʾs��
�۵�F������������5ʱ��Ҳ����m�Ĵ���ʽ�ֱ��ʾPE��MF��Ȼ��Ϳ����ú�m�Ĵ���ʽ��ʾs��
��2������PM����PH��x����H����MG��x����G��Ȼ��֤����PBH�ա�MBG����������ȫ�������ε��������M�����꣬���Ϳ������������C2�Ľ���ʽ��
��3�����ȷֱ���m��ʾE��F��������꣬Ȼ�����ۣ�
�ٵ�E���������С��-5ʱ����m�Ĵ���ʽ�ֱ��ʾPE��MF��Ȼ��Ϳ����ú�m�Ĵ���ʽ��ʾs��
�ڵ�E������������-5��F���������С��5ʱ��Ҳ��m�Ĵ���ʽ�ֱ��ʾPE��MF��Ȼ��Ϳ����ú�m�Ĵ���ʽ��ʾs��
�۵�F������������5ʱ��Ҳ����m�Ĵ���ʽ�ֱ��ʾPE��MF��Ȼ��Ϳ����ú�m�Ĵ���ʽ��ʾs��
��� �⣺��1����������C1��y=ax2+4ax+4a-5=a��x+2��2-5��
�⣺��1����������C1��y=ax2+4ax+4a-5=a��x+2��2-5��
�ඥ��P������Ϊ��-2��-5��
�ߵ�B��1��0����������C1�ϣ���a=
��������C1�Ľ���ʽΪy=
x2+
x-
��
��2������PM����PH��x����H����MG��x����G
�ߵ�P��M���ڵ�B�����ĶԳ�
��PM����B����PB=MB
���PBH�ա�MBG
��MG=PH=5��BG=BH=3
�ඥ��M������Ϊ��4��5��
��������C2�ı���ʽΪy=-
��x-4��2+5��
��3��������ã�E��-2��
+m����F��4��-
+m����HG=6
�ٵ�E���������С��-5ʱ��
PE=-5-(
+m)=-
-m��MF=5-(-
+m)=
-m��
��s=
(-
-m+
-m)��6=-6m+
��
�ڵ�E������������-5��F���������С��5ʱ��
PE=
+m-(-5)=
+m��MF=5-(-
+m)=
-m��
��s=
��
�۵�F������������5ʱ��
PE=
+m-(-5)=
+m��MF=-
+m-5=-
+m
��s=6m-
��
 �⣺��1����������C1��y=ax2+4ax+4a-5=a��x+2��2-5��
�⣺��1����������C1��y=ax2+4ax+4a-5=a��x+2��2-5���ඥ��P������Ϊ��-2��-5��
�ߵ�B��1��0����������C1�ϣ���a=
| 5 |
| 9 |
��������C1�Ľ���ʽΪy=
| 5 |
| 9 |
| 20 |
| 9 |
| 25 |
| 9 |
��2������PM����PH��x����H����MG��x����G
�ߵ�P��M���ڵ�B�����ĶԳ�
��PM����B����PB=MB
���PBH�ա�MBG
��MG=PH=5��BG=BH=3
�ඥ��M������Ϊ��4��5��
��������C2�ı���ʽΪy=-
| 5 |
| 9 |
��3��������ã�E��-2��
| 6 |
| 5 |
| 12 |
| 5 |
�ٵ�E���������С��-5ʱ��
PE=-5-(
| 6 |
| 5 |
| 31 |
| 5 |
| 12 |
| 5 |
| 37 |
| 5 |
��s=
| 1 |
| 2 |
| 31 |
| 5 |
| 37 |
| 5 |
| 18 |
| 5 |
�ڵ�E������������-5��F���������С��5ʱ��
PE=
| 6 |
| 5 |
| 31 |
| 5 |
| 12 |
| 5 |
| 37 |
| 5 |
��s=
| 204 |
| 5 |
�۵�F������������5ʱ��
PE=
| 6 |
| 5 |
| 31 |
| 5 |
| 12 |
| 5 |
| 37 |
| 5 |
��s=6m-
| 18 |
| 5 |
�����������Ƕ��κ������ۺ��⣬�ֱ��˴���ϵ����ȷ�������Ľ���ʽ�����κ�����ͼ������ʡ�ȫ�������ε��ж����ʼ���ԳƵ����ʣ��ۺ��Ժ�ǿ��Ҫ��ѧ���к�ǿ���ۺϷ��������������������ͬʱҪ��ѧ���Ļ���֪ʶ�Ǻ������ģ�

��ϰ��ϵ�д�
�����Ŀ
 ��2010•��ɽ��һģ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��l1��
��2010•��ɽ��һģ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��l1��