题目内容
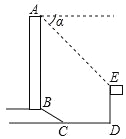
【题目】已知Rt△ABD中,边AB=OB=1,∠ABO=90°
问题探究:
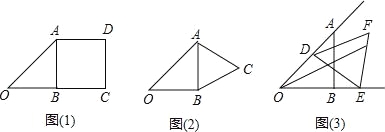
(1)以AB为边,在Rt△ABO的右边作正方形ABC,如图(1),则点O与点D的距离为 .
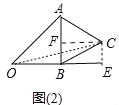
(2)以AB为边,在Rt△ABO的右边作等边三角形ABC,如图(2),求点O与点C的距离.
问题解决:
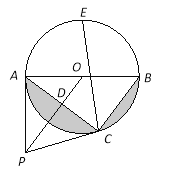
(3)若线段DE=1,线段DE的两个端点D,E分别在射线OA、OB上滑动,以DE为边向外作等边三角形DEF,如图(3),则点O与点F的距离有没有最大值,如果有,求出最大值,如果没有,说明理由.
【答案】(1)、![]() ;(2)、
;(2)、![]() ;(3)、
;(3)、![]() .
.
【解析】
试题分析:(1)、如图1中,连接OD,在Rt△ODC中,根据OD=![]() 计算即可.(2)、如图2中,作CE⊥OB于E,CF⊥AB于F,连接OC.在Rt△OCE中,根据OC=
计算即可.(2)、如图2中,作CE⊥OB于E,CF⊥AB于F,连接OC.在Rt△OCE中,根据OC=![]() 计算即可.(3)、如图3中,当OF⊥DE时,OF的值最大,设OF交DE于H,在OH上取一点M,使得OM=DM,连接DM.分别求出MH、OM、FH即可解决问题.
计算即可.(3)、如图3中,当OF⊥DE时,OF的值最大,设OF交DE于H,在OH上取一点M,使得OM=DM,连接DM.分别求出MH、OM、FH即可解决问题.
试题解析:(1)、如图1中,连接OD,
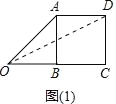
∵四边形ABCD是正方形, ∴AB=BC=CD=AD=1,∠C=90° 在Rt△ODC中,∵∠C=90°,OC=2,CD=1,
∴OD=![]() =
=![]() =
=![]() .
.
(2)、如图2中,作CE⊥OB于E,CF⊥AB于F,连接OC.
∵∠FBE=∠E=∠CFB=90°, ∴四边形BECF是矩形, ∴BF=CF=![]() ,CF=BE=
,CF=BE=![]() ,
,
在Rt△OCE中,OC=![]() =
= =
=![]() .
.
(3)、如图3中,当OF⊥DE时,OF的值最大,设OF交DE于H,在OH上取一点M,使得OM=DM,连接DM.

∵FD=FE=DE=1,OF⊥DE, ∴DH=HE,OD=OE,∠DOH=![]() ∠DOE=22.5°, ∵OM=DM,
∠DOE=22.5°, ∵OM=DM,
∴∠MOD=∠MDO=22.5°, ∴∠DMH=∠MDH=45°, ∴DH=HM=![]() , ∴DM=OM=
, ∴DM=OM=![]() ,
,
∵FH=![]() =
=![]() , ∴OF=OM+MH+FH=
, ∴OF=OM+MH+FH=![]() +
+![]() +
+![]() =
=![]() .
.
∴OF的最大值为![]() .
.