Question

【题目】【问题情境】

已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？

【数学模型】

设该矩形的长为x，周长为y，则y与x的函数表达式为y=2（x+ ）（x＞0）．

【探索研究】

小彬借鉴以前研究函数的经验，先探索函数y=x+的图象性质．

（1）结合问题情境，函数y=x+ 的自变量x的取值范围是x＞0，下表是y与x的几组对应值．

① 写出m的值；

②画出该函数图象，结合图象，得出当x=________时，y有最小值，y最小=________；

提示：在求二次函数y=ax2+bx+c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．试用配方法求函数y=x+ （x＞0）的最小值，解决问题（2）．

（2）【解决问题】

直接写出“问题情境”中问题的结论．

Answer 1

【答案】（1）①4；②1；2；（2）矩形的面积为a（a为常数，a＞0），当该矩形的长为时，它的周长最小，最小值是．

【解析】试题分析：（1）①由题意易求出m的值，②观察函数图像可知，利用完全平方公式将函数解析式进行配方，即可得到函数的最小值．

（2）根据完全平方公式将函数解析式进行配方，即可求出结果．

试题解析：解：（1）①由题意m=4；

②函数y=x+的图象如图：

y=x+==

∵x＞0，所以≥0，

所以当x=1时， 的最小值为0，

∴当x=1时，函数y=x+（x＞0）的最小值是2．

（2）∵y==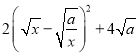，∴当时，即x=时，y的值最小，最小值为．

答：矩形的面积为a，当矩形的长为时，它的周长最小，最小值为．