题目内容
【题目】如图,点![]() 在
在![]() 的边
的边![]() 上,过点
上,过点![]() 作
作![]() 的平行线
的平行线![]() ,如果
,如果![]() ,那么
,那么![]() 的度数为__________.
的度数为__________.

【答案】(1)①中线;②是;(2)见解析;(3)![]() .
.
【解析】
(1)①根据中线及二分线的定义即可求解;
②先由AD是BC边上的中线可得S△ABD=S△ACD,再根据![]() 可得S四边形ACFE=S△BEF即可求解;
可得S四边形ACFE=S△BEF即可求解;
(2)先证△CDG≌△EAG可得S△CDG=S△EAG,再根据F是EB的中点即可求解;
(3)分别证明△AEB≌△CDE,△AEB≌△EBH,△MHB≌△MAE,然后得出S△MHB=S△MAE,再根据全等三角形的性质及二分线定义即可求解.
(1)①三角形的中线、高线、角平分线中,一定是三角形的二分线的是中线,
故答案为中线;
②∵AD是BC边上的中线,
∴S△ABD=S△ACD,
又∵![]() ,
,
∴S四边形BEGD=S四边形AGFC,
∴S四边形BEGD+![]() =S四边形AGFC+
=S四边形AGFC+![]() ,
,
∴![]() =S四边形AEFC,
=S四边形AEFC,
所以EF是△ABC的一条二分线,故答案为是;
(2)∵点G是AD的中点,
∴GD=AG,
∵AB∥DC,
∴∠D=∠GAE,
在△CDG和△EAG中,
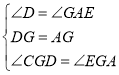 ,
,
∴△CDG≌△EAG(ASA),
∴S△CDG=S△EAG,
∵点F是EB的中点,
∴S△CFE=S△CBF,
即S△AGE+S四边形AGCF=S△CBF,
∴S△CDG+S四边形AGCF=S△CBF,即S四边形ADCF=S△CBF,
∴CF是四边形ABCD的二分线;
(3)如图,延长CB于点H,使得BH=AE,连接EH交AB于点M,
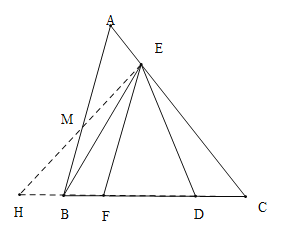 ,
,
∵AB=BC,
∴∠A=∠C,
∵∠BED=∠A,
∴∠AEB=∠CDE,
在△AEB和△CDE中,
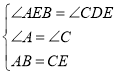 ,
,
∴△AEB≌△CDE(AAS),
∴AE=CD,
∴BH=CD,
∴DH=CB,
∵CB=CE,
∴∠CBE=∠CEB,
∴∠HBE=∠AEB,
在△EBH和△BEA中,
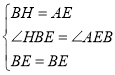 ,
,
∴△AEB≌△EBH(SAS),
∴∠H=∠A,
在△MBH和△MEA中,
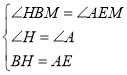 ,
,
∴△MHB≌△MAE(ASA),
∴S△HMB+S四边形MBFE=S△AME+S四边形MBFE,即S△HEF=S四边形ABFE,
∵EF是四边形ABDE的一条二分线,
∴S四边形ABFE=S△DEF,
∴S△HEF=S△DEF,
∴DF=![]() DH=
DH=![]() CB=
CB=![]() .
.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案






