题目内容
【题目】已知关于x的一元二次方程mx2－(m+2)x＋2=0（m≠0）
(1)求证：方程一定有两个实数根；
(2)若此方程的两根为不相等的整数，求整数m的值．
【答案】（1）见详解；（2）-1，-2，1
【解析】
（1）先计算判别式的值，然后根据判别式的意义即可得到方程总有两个不相等的实数根；
（2）利用求根公式法解方程得到x1＝1，x2＝
，然后利用有理数的整除性确定m的值．
（1）证明：∵一元二次方程mx2－(m+2)x＋2=0（m≠0）
∴Δ=[-(m+2)] 2-4×2m=m2+4m+4-8m=(m-2)2，
∵m≠0
∴Δ=(m-2)2≥0
∴方程一定有两个实数根；
（2）解：由求根公式得，x1=1，x2=
∵方程的两根为不相等的整数，且m为整数
∴是整数，而m≠0
∴m=±1，±2,
而当m=2时，x1=x2=1，(舍去)
∴整数m为1，-1，-2
故答案为：1，-1，-2．
【题目】第二十四届冬季奥林匹克运动会将于2022年在北京市和张家口市举行．为了调查学生对冬奥知识的了解情况，从甲、乙两校各随机抽取20名学生进行了相关知识测试，获得了他们的成绩（百分制），并对数据（成绩）进行了整理、描述和分析．下面给出了部分信息．
a．甲校20名学生成绩的频数分布表和频数分布直方图如下：
甲校学生样本成绩频数分布表
成绩m（分） | 频数（人数） | 频率 |
| 1 | 0.05 |
| c | 0.10 |
| 3 | 0.15 |
| a | b |
| 6 | 0.30 |
合计 | 20 | 1.0 |
表1
图1
b．甲校成绩在
的这一组的具体成绩是：81 81 89 83 89 82 83 89
c．甲、乙两校成绩的平均分、中位数、众数、方差如下：
学校 | 平均分 | 中位数 | 众数 | 方差 |
甲 | 84 | n | 89 | 129.7 |
乙 | 84.2 | 85 | 85 | 138.6 |
表2
根据以上图表提供的信息，解答下列问题：
（1）表1中a=______；表2中的中位数n =_______；
（2）补全图1甲校学生样本成绩频数分布直方图；
（3）在此次测试中，某学生的成绩是84分，在他所属学校排在前10名，由表中数据可知该学生是______校的学生（填“甲”或“乙”），理由是________；
（4）假设甲校1000名学生都参加此次测试，若成绩80分及以上为优秀，估计成绩优秀的学生人数为_______人．
【题目】有这样一个问题：探究函数
的图象与性质．小华根据学习函数的经验，对函数的图象与性质进行了探究．下面是小华的探究过程，请补充完整：
(1)函数的自变量x的取值范围是___________；
(2)下表是y与x的几组对应值．m的值为_______；
x | -2 |
| -1 |
|
|
| 1 | 2 | 3 | 4 | … |
y | 0 |
| m |
|
|
|
| 1 |
|
| … |
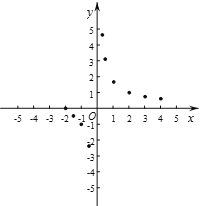
(3)如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
(4)结合函数的图象，写出该函数的一条性质：____________．
(5)结合函数图象估计
的解的个数为_______个．
