题目内容
【题目】在边长为4的等边△ABC中.
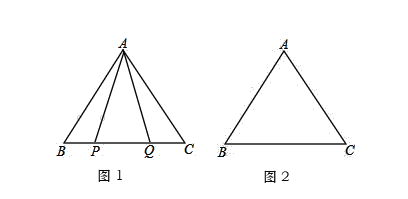
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=18°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.依题意将图2补全,并求证PA=PM.
(3)在(2)中,当AM的值最小时,直接写出CM的长.
【答案】(1)78°;(2)见解析;(3)2.
【解析】
(1)根据等腰三角形的性质得到∠APQ=∠AQP,由邻补角的定义得到∠APB=∠AQC,根据三角形外角的性质即可得到结论;
(2)如图2根据等腰三角形的性质得到∠APQ=∠AQP,由邻补角的定义得到∠APB=∠AQC,由点Q关于直线AC的对称点为M,得到AQ=AM,∠OAC=∠MAC,等量代换得到∠MAC=∠BAP,推出△APM是等边三角形,根据等边三角形的性质即可得到结论.
(3)因为AM=AP,所以当AP⊥BC时,AM的值最小,此时P、Q重合,由此即可解决问题;
(1)∵AP=AQ,
∴∠APQ=∠AQP,
∴∠APB=∠AQC,
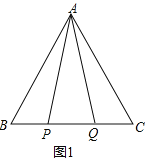
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠BAP=∠CAQ=18°,
∴∠AQB=∠APQ=∠BAP+∠B=78°;
(2)如图2,∵点Q关于直线AC的对称点为M,
∴AQ=AM,∠QAC=∠MAC,
∵∠BAP=∠CAQ,
∴∠MAC=∠BAP,
∴∠BAP+∠PAC=∠MAC+∠CAP=60°,
∴∠PAM=60°,
∵AP=AQ,
∴AP=AM,
∴△APM是等边三角形,
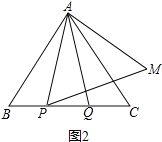
∴AP=PM.
(3)∵AM=AP,
∴当AP⊥BC时,AM的值最小,
∴此时P、Q重合,CM=CQ=QB=2.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目