题目内容
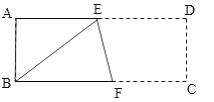
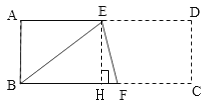
【题目】已知，如图长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则下列结论：①△ABE的面积为6cm2，②BF的长为5cm，③EF的长为
cm，④四边形CDEF的面积是13.5cm2.其中正确的个数有（ ）
A.4B.3C.2D.1
【答案】A
【解析】
①由勾股定理构造方程可求得AE，则△ABE的面积可求；②由折叠及平行线性质，可证明BD=BE，则问题可解；③过点E作ED⊥BC于H，利用勾股定理求EF；④由①、②，可求得ED、FC，则四边形CDEF的面积可求；
解：①由折叠可知，BE=DE
∵AD=9
∴BE=9-AE
RtΔABE中，
AB2+AE2=BE2
∴32+AE2=（9-AE）2
∴AE=4
∴△ABE的面积为
∴△ABE的面积为6cm2
故①正确；
②由①DE=BE=5
由折叠可知, ∠BEF=∠DEF
∵AD∥BC
∴∠BFE=∠DEF
∴∠BFE=∠BEF
∴BF=BE=5
故BF的长为5cm
②正确；
③过点E作ED⊥BC于H
由①、②可知，HF=1，EH=AB=3
则Rt△EHF中：
EF=
则EF的长为
cm
③正确；
④由①、②可知，ED=5，FC=BC-BF=4
∴四边形CDEF的面积：
四边形CDEF的面积是13.5cm2.
④正确；
故应选A
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
