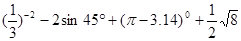题目内容
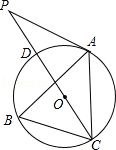
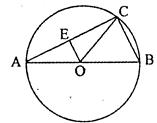
已知△ABC中，∠C=90°，tanA=
，D是AC上一点，∠CBD=∠A，则sin∠ABD=【 】。
，D是AC上一点，∠CBD=∠A，则sin∠ABD=【 】。A． | B． | C． | D． |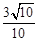
A。
如图，作DE⊥AB于点E。
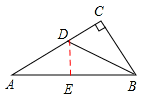
∵∠CBD=∠A，∴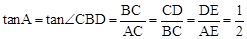
。
设CD=a，则BC=2a，AC=4a，AD=AC-CD=3a，
在Rt△BCD中，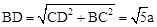
。
在Rt△ABC中，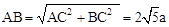
。
在Rt△ADE中，设DE=x，则AE=2x，
∵AE2+DE2=AD2，即x2+（2x）2=9a2，解得：x=
，即DE=。
在Rt△BDE中，
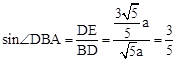。故选A。
∵∠CBD=∠A，∴
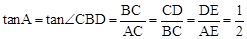。设CD=a，则BC=2a，AC=4a，AD=AC-CD=3a，
在Rt△BCD中，
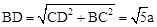。在Rt△ABC中，
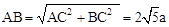。在Rt△ADE中，设DE=x，则AE=2x，
∵AE2+DE2=AD2，即x2+（2x）2=9a2，解得：x=
，即DE=。在Rt△BDE中，
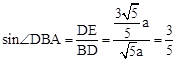。故选A。
练习册系列答案
通城学典默写能手系列答案
相关题目
≈1.73，精确到个位）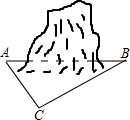
．
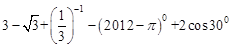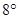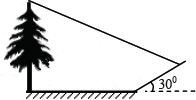
和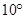
，大灯A与地面的距离为1m，则该车大灯照亮地面的宽度BC是________m .（不考虑其它因素）（参考数据：
）
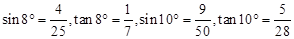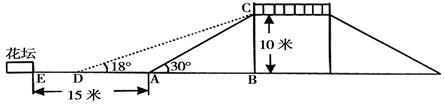
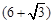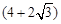米
米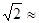
1.414，
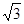≈1.732)
