题目内容
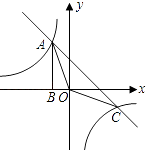
【题目】如图,Rt△ABO的顶点A是双曲线y1= ![]() 与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO= ![]() .
. 
(1)求这两个函数的解析式;
(2)求△AOC的面积;
(3)直接写出使y1>y2成立的x的取值范围.
【答案】
(1)解:设A点坐标为(x,y),且x<0,y>0,
则S△ABO= ![]() |BO||BA|=
|BO||BA|= ![]() (﹣x)y=
(﹣x)y= ![]() ,
,
∴xy=﹣3,
又∵y= ![]() ,
,
即xy=k,
∴k=﹣3.
∴所求的两个函数的解析式分别为y=﹣ ![]() ,y=﹣x+2
,y=﹣x+2
(2)解:由y=﹣x+2,
令x=0,得y=2.
∴直线y=﹣x+2与y轴的交点D的坐标为(0,2),
∵A、C在反比例函数的图象上,
∴ 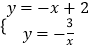 ,解得
,解得 ![]() ,
, ![]() ,
,
∴交点A为(﹣1,3),C为(3,﹣1),
∴S△AOC=S△ODA+S△ODC= ![]() OD(|x1|+|x2|)=
OD(|x1|+|x2|)= ![]() ×2×(3+1)=4
×2×(3+1)=4
(3)解:使y1>y2成立的x的取值范围是:﹣1<x<0或x>3
【解析】(1)欲求这两个函数的解析式,关键求k值.根据反比例函数性质,k绝对值为3且为负数,由此即可求出k;(2)由函数的解析式组成方程组,解之求得A、C的坐标,然后根据S△AOC=S△ODA+S△ODC即可求出;(3)根据图象即可求得.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目