题目内容
【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P、Q两点停止运动.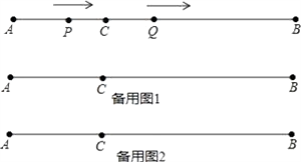
(1)AC=cm,BC=cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,PQ=1cm.
【答案】
(1)4;8
(2)解:由题意可知:AP=3t,PQ=4﹣(3t﹣t),
则3t=4﹣(3t﹣t),
解得:t= ![]() .
.
答:当t= ![]() 时,AP=PQ
时,AP=PQ
(3)解:∵点P、Q相距的路程为1cm,
∴(4+t)﹣3t=1(相遇前)或3t﹣(4+t)=1(第一次相遇后),
解得t= ![]() 或t=
或t= ![]() ,
,
当到达B点时,第一次相遇后点P、Q相距的路程为1cm,
3t+4+t=12+12﹣1
解得:t= ![]() .
.
答:当t为 ![]() ,
, ![]() ,
, ![]() 时,PQ=1cm
时,PQ=1cm
【解析】(1)∵AB=12cm,点C是线段AB上的一点,BC=2AC,
∴AC+BC=3AC=AB=12cm,
∴AC=4cm,BC=8cm;
(1)根据AB=12cm,点C是线段AB上的一点,BC=2AC,得出AB=AC+BC=3AC=12cm ,进而得出答案AC=4cm,BC=8cm ;
(2)由题意可知:AP=3t,PQ=4﹣(3t﹣t),然后由AP=PQ;列出关于t的方程,求解得出t的值 ;
(3)此题分三种情况:①相遇前,由PQ=1列出方程(4+t)﹣3t=1 ;②第一次相遇后由PQ=1列出方程3t﹣(4+t)=1 ,③当到达B点时,第一次相遇后点P、Q相距的路程为1cm,列出方程3t+4+t=12+12﹣1 ,分别解方程求出t的值即可 。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目