题目内容
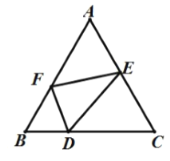
【题目】(1)如图1,求证:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等;
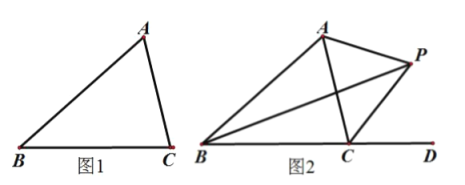
(2)如图2,若![]() 的平分线与
的平分线与![]() 外角
外角![]() 的平分线相交于点
的平分线相交于点![]() 连接
连接![]() ,若
,若![]() ,则
,则![]() 是 度.
是 度.
【答案】(1)详见解析;(2)59°
【解析】
(1)设∠A和∠B的平分线交于点O,连接OC,作OG,OE,OF与各边垂直,根据角平分线的性质和判定判定定理可得;
(2)作PE⊥BC,PF⊥AC,PG⊥AB,根据角平分线性质和判定可得P在∠GAC的平分线上,根据临补角定义可得.
(1)证明:设∠A和∠B的平分线交于点O,连接OC,作OG,OE,OF与各边垂直,
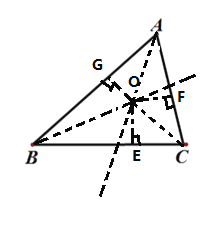
∵AO平分∠BAC,
∴O到AB、AC的距离相等,即OG=OF
同理O到BA、BC的距离相等,即OG=OE
∴OG=OE=OF,O到CA、CB距离相等,
∴O在∠BCA的平分线上,
∴三角形三条边的三条角平分线相交于一点,这一点到三边的距离相等;
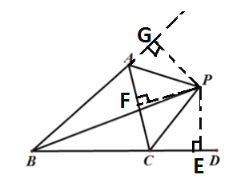
(2)解:作PE⊥BC,PF⊥AC,PG⊥AB
因为CP平分∠ACD
BP平分∠ABC
所以PB=PF=PG
所以P在∠GAC的平分线上,
所以∠PAC=![]() ∠GAC
∠GAC
=![]()
![]()

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目