题目内容
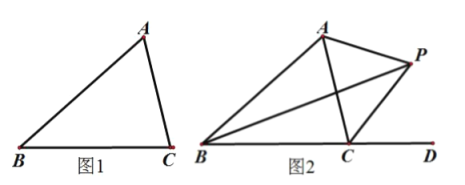
【题目】已知：如图BE//CF，BE、CF分别平分∠ABC和∠BCD, 求证：AB//CD
证明：∵ BE、CF分别平分∠ABC和∠BCD（已知）
∴ ∠1=
∠ ∠2=
∠ （ ）
∵ BE//CF（ ）
∴ ∠1=∠2（ ）
∴ 
∠ABC=
∠BCD
即∠ABC=∠BCD
∴ AB//CD（ ）
【答案】 解：∵BE、CF分别平分∠ABC和∠BCD（已知），
∴∠1=
∠ABC，∠2=∠BCD（角平分线的定义）；
∵BE∥CF（已知），
∴∠1=∠2（两直线平行，内错角相等），
∴∠ABC=∠BCD，
即∠ABC=∠BCD，
∴AB∥CD（内错角相等，两直线平行）．
【解析】先利用角平分线的定义填空，再根据平行线的性质和判定填空．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
