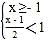题目内容
【题目】某商场计划从一厂家购进若干部新型手机以满足市场需求.已知该厂家生产三种不同型号的手机,出厂价分别是甲种型号手机1800元/部,乙种型号手机600元/部,丙种型号手机1200元/部.商场在经销中,甲种型号手机可赚200元/部,乙种型号手机可赚100元/部,丙种型号手机可赚120元/部.
(1)若商场用6万元同时购进两种不同型号的手机共40部,并恰好将钱用完,请你通过计算分析进货方案;
(2)在(1)的条件下,求盈利最多的进货方案.
【答案】(1)有两种进货方案:方案一,甲种型号手机购进30部,乙种型号手机购进10部,方案二,甲种型号手机购进20部,丙种型号手机购进20部;(2)购进甲种型号手机30部,乙种型号手机10部盈利最多.
【解析】
(1)商场用6万元同时购进两种不同型号的手机有三类不同的方案:①购进甲乙两种,②乙丙两种,③购进甲丙两种.然后根据购进的两种手机的部数和=40,购机两种手机用的总费用=6万元,这两个等量关系来列出方程组,解方程组即可.
(2)根据(1)得出的方案,计算出各方案的盈利额,然后比较哪种盈利较多;
(1)设购进甲种型号手机x部,乙种型号手机y部,丙种型号手机z部.
根据题意,得
①![]() 解得
解得![]()
②![]() 解得
解得![]()
③![]()
解得![]() (不合题意,舍去)
(不合题意,舍去)
故有两种进货方案:方案一,甲种型号手机购进30部,乙种型号手机购进10部;方案二,甲种型号手机购进20部,丙种型号手机购进20部.
(2)方案一盈利:200×30+100×10=7000(元);
方案二盈利:200×20+120×20=6400(元).
因为7000元>6400元,
所以购进甲种型号手机30部,乙种型号手机10部盈利最多.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目