题目内容
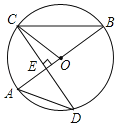
【题目】(1)如图1,Rt△ABM和Rt△ADN的斜边分别为正方形的边AB和AD,其中AM=AN,线段MN与线段AD相交于点T,若AD=3AT,则tan∠ABM= ;

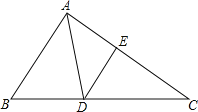
(2)如图2,在菱形ABCD中,CD=6,∠ADC=60°,菱形形内部有一动点P,满足S△PAB=![]() S菱形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为 .
S菱形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为 .
【答案】(1)tan∠ABM=![]() ;(2)PA+PB的最小值为2
;(2)PA+PB的最小值为2![]() .
.
【解析】
(1)先利用HL证明Rt△ABM≌Rt△AND,再证明△DNT∽△AMT,可得![]() =
=![]() ,由AD=3AT,推出
,由AD=3AT,推出![]() =
=![]() ,在Rt△ABM中,tan∠ABM=
,在Rt△ABM中,tan∠ABM=![]() =
=![]() =
=![]() ;
;
(2) 首先由S△PAB=![]() S菱形ABCD,,得出动点P在与AB平行且与AB的距离是2
S菱形ABCD,,得出动点P在与AB平行且与AB的距离是2![]() 的直线l上,作A关于直线l的对称点A′,连接AA′,连接BA′,则BA′的长就是所求的最短距离.然后在直角三角形ABA′中,由勾股定理求得BA′的值,即PA+PB的最小值.
的直线l上,作A关于直线l的对称点A′,连接AA′,连接BA′,则BA′的长就是所求的最短距离.然后在直角三角形ABA′中,由勾股定理求得BA′的值,即PA+PB的最小值.
(1)∵AD=AB,AM=AN,∠AMB=∠AND=90°,
∴Rt△ABM≌Rt△AND(HL).
∴∠DAN=∠BAM,DN=BM,
∵∠BAM+∠DAM=90°;∠DAN+∠ADN=90°,
∴∠DAM=∠ADN,
∴ND∥AM,
∴△DNT∽△AMT,
∴![]() =
=![]() ,
,
∵AT=![]() AD,
AD,
∴![]() =
=![]() ,
,
在Rt△ABM中,tan∠ABM=![]() =
=![]() =
=![]() ;
;
故答案为:![]() ;
;
(2)∵四边形ABCD是菱形,
∴AB=CD=6,
连接AC,BD交于O,
∴AC⊥BD,
∵∠ADC=60°,
∴∠CDO=30°,
∴DO=3![]() ,OC=3,
,OC=3,
∴BD=6![]() ,AC=6,
,AC=6,
∴S菱形ABCD=![]() ×6×6
×6×6![]() =18
=18![]() ;
;
设△ABP中AB边上的高是h,
∵S△PAB=![]() S菱形ABCD,
S菱形ABCD,
∴![]() ABh=
ABh=![]() ×18
×18![]() =6
=6![]() ,
,
∴h=2![]() ,
,
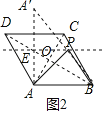
∴动点P在与AB平行且与AB的距离是2![]() 的直线l上,如图,作A关于直线l的对称点A′,连接AA′,连接BA′,则BA′的长就是所求的最短距离.
的直线l上,如图,作A关于直线l的对称点A′,连接AA′,连接BA′,则BA′的长就是所求的最短距离.
在Rt△ABE中,∵AB=6,AA′=4![]() ,
,
∴BA′=![]() =2
=2![]() ,
,
即PA+PB的最小值为2![]() .
.
故答案为:2![]() .
.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案