题目内容
如图,抛物线y=x
2+bx+c(b≤0)的图象与x轴交于A,B两点,与y轴交于点C,其中点A的

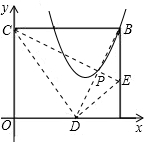
坐标为(-2,0);直线x=1与抛物线交于点E,与x轴交于点F,且45°≤∠FAE≤60度.
(1)用b表示点E的坐标;
(2)求实数b的取值范围;
(3)请问△BCE的面积是否有最大值?若有,求出这个最大值;若没有,请说明理由.
(1)∵抛物线y=x
2+bx+c过A(-2,0),
∴c=2b-4
∵点E在抛物线上,
∴y=1+b+c=1+2b-4+b=3b-3,
∴点E的坐标为(1,3b-3).
(2)由(1)得EF=3-3b,
∵45°≤∠FAE≤60°,AF=3,
tan60°=
=
,
∴b=1-
,
∴1-
≤b≤0.
(3)△BCE的面积有最大值,
∵y=x
2+bx+c的对称轴为x=-
,A(-2,0),
∴点B的坐标为(2-b,0),
由(1)得C(0,2b-4),
而S
△BCE=S
梯形OCEF+S
△EFB-S
△OCB=
(OC+EF)•OF+
EF•FB-
OB•OC
=
[(4-2b)+(3-3b)]×1+
(3-3b)(1-b)-
(2-b)•(4-2b)
=
(b
2-3b+2),
∵y=
(b
2-3b+2)的对称轴是b=
,1-
≤b≤0
∴当b=1-
时,S
△BCE取最大值,
其最大值为
[(1-
)
2-3(1-
)+2]=
.
练习册系列答案
相关题目
 坐标为(-2,0);直线x=1与抛物线交于点E,与x轴交于点F,且45°≤∠FAE≤60度.
坐标为(-2,0);直线x=1与抛物线交于点E,与x轴交于点F,且45°≤∠FAE≤60度. 坐标为(-2,0);直线x=1与抛物线交于点E,与x轴交于点F,且45°≤∠FAE≤60度.
坐标为(-2,0);直线x=1与抛物线交于点E,与x轴交于点F,且45°≤∠FAE≤60度.

 上,请说明理由.
上,请说明理由.