题目内容
【题目】如图,矩形ABCD的边AD是菱形AEDF的一条对角线,且点E在矩形ABCD的边BC上.
(1)求证:△ABE≌△DCE;
(2)直接写出当矩形边长AD与AB之间满足什么关系时,菱形AEDF为正方形.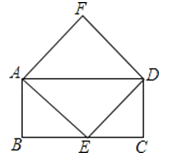
【答案】(1)证明:∵四边形ABCD是矩形,
∴AB=DC,∠B=∠C=90°,AD=BC,
∵四边形AEDF是菱形,
∴AE=DE,
在Rt△ABE和Rt△DCE中,![]() ,
,
∴Rt△ABE≌Rt△DCE(HL);
(2)解:当AD=2AB时,菱形AEDF为正方形;理由如下:
∵Rt△ABE≌Rt△DCE,
∴BE=CE,∠AEB=∠DEC,
∵AD=2AB,AD=BC,
∴AB=BE,
∴△ABE是等腰直角三角形,
∴∠AEB=45°,
∴∠DEC=45°,
∴∠AED=180°﹣45°﹣45°=90°,
∴菱形AEDF为正方形.
【解析】(1)由矩形的性质得出AB=DC,∠B=∠C=90°,由菱形的性质得出AE=DE,由HL证明Rt△ABE≌Rt△DCE即可;
(2)由全等三角形的性质得出BE=CE,∠AEB=∠DEC,由AD=2AB,证出△ABE是等腰直角三角形,得出∠AEB=45°,证出∠AED=90°,即可得出菱形AEDF为正方形.
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等).

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目