题目内容
【题目】如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=![]() CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为
CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为 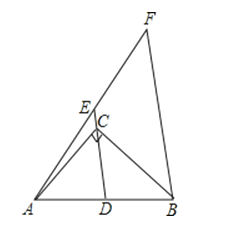
【答案】8
【解析】解:∵∠ACB=90°,D为AB的中点,AB=6,
∴CD=![]() AB=3;
AB=3;
又∵CE=![]() CD,
CD,
∴CE=![]()
![]() =1,
=1,
∴ED=CE+CD=1+3=4;
又∵BF∥DE,点D是AB的中点,
∴ED是△AFB的中位线.
∴BF=2ED=2×4=8,
即BF的长为8.
故答案为:8.
首先根据直角三角形斜边上中线的性质,求出CD的长度是多少;然后根据CE=![]() CD,求出CE的长度是多少,进而求出ED的长度是多少;最后判断出ED是△AFB的中位线,根据三角形中位线定理,求出BF的长为多少即可.
CD,求出CE的长度是多少,进而求出ED的长度是多少;最后判断出ED是△AFB的中位线,根据三角形中位线定理,求出BF的长为多少即可.

练习册系列答案
相关题目