题目内容
【题目】探究题
（1）【证法回顾】
证明：三角形中位线定理．
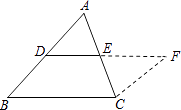
已知：如图1，DE是△ABC的中位线．
求证：DE∥BC，DE= 
BC．
证明：添加辅助线：如图1，在△ABC中，延长DE （D、E分别是AB、AC的中点）到点F，使得EF=DE，连接CF；请继续完成证明过程：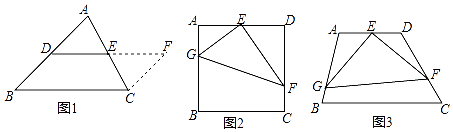
（2）【问题解决】
如图2，在正方形ABCD中，E为AD的中点，G、F分别为AB、CD边上的点，若AG=2，DF=3，∠GEF=90°，求GF的长．
（3）【拓展研究】如图3，在四边形ABCD中，∠A=105°，∠D=120°，E为AD的中点，G、F分别为AB、CD边上的点，若AG=3 
，DF=2，∠GEF=90°，求GF的长．
【答案】
（1）
证明：如图，延长DE 到点F，使得EF=DE，连接CF
在△ADE和△CFE中，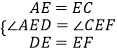 
，
∴△ADE≌△CFE（SAS），
∴∠A=∠ECF，AD=CF，
∴CF∥AB，
又∵AD=BD，
∴CF=BD，
∴四边形BCFD是平行四边形，
∴DE∥BC，DE= 
BC．
故答案为：DE∥BC，DE= BC
（2）
如图2，延长GE、FD交于点H，
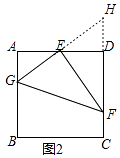
∵E为AD中点，
∴EA=ED，且∠A=∠EDH=90°，
在△AEG和△DEH中，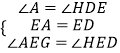 
∴△AEG≌△DEH（ASA），
∴AG=HD=2，EG=EH，
∵∠GEF=90°，
∴EF垂直平分GH，
∴GF=HF=DH+DF=2+3=5；
（3）
如图3，过点D作AB的平行线交GE的延长线于点H，过H作CD的垂线，垂足为P，连接HF，
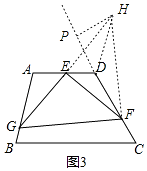
同（1）可知△AEG≌△DEH，GF=HF，
∴∠A=∠HDE=105°，AG=HD= 
，
∵∠ADC=120°，
∴∠HDF=360°﹣105°﹣120°=135°，
∴∠HDP=45°，
∴△PDH为等腰直角三角形，
∴PD=PH=3，
∴PF=PD+DF=3+2=5，
在Rt△HFP中，∠HPF=90°，HP=3，PF=5，
∴HF= 
═ 
∴GF= ．
【解析】（1）利用“边角边”证明△ADE和△CEF全等，根据全等三角形对应边相等可得AD=CF，然后判断出四边形BCFD是平行四边形，根据平行四边形的性质可得；（2）先判断出△AEG≌△DEH（ASA）进而判断出EF垂直平分GH，即可得出结论；（3）先求出AG=HD= ，进而判断出△PDH为等腰直角三角形，再用勾股定理求出HF即可得出结论．
【考点精析】本题主要考查了全等三角形的性质和三角形中位线定理的相关知识点，需要掌握全等三角形的对应边相等; 全等三角形的对应角相等；连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半才能正确解答此题．
