Question

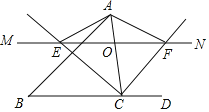
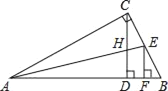
【题目】如图，Rt△ABC中，∠ACB＝90°，CD⊥AB，∠CAB的平分线AE交CD于点H、交CB于点E，EF⊥AB于点F，则下列结论中不正确的是（　　）

A. ∠ACD＝∠BB. CH＝CE＝EFC. CH＝HDD. AC＝AF

Answer 1

【答案】C

【解析】

根据角平分线的性质可得CE=EF，由于AE是公共边，利用三角形全等的判定定理，从而可得△AEF≌△AEC；利用全等三角形的性质即可解得.

对于选项A，

∵CD⊥AB，

∴∠CAD+∠ACD=90°.

∵△ABC是直角三角形，

∴∠CAD+∠ABC=90°.

∵∠CAD+∠ABC=90°，∠CAD+∠ACD=90°，

∴∠ACD=∠ABC.

所以选项A不符合题意；

对于选项B，

∵AE是∠BAC的角平分线，∠ACE=90°，EF⊥AB，

∴CE=EF.

∵∠ACE=90°，EF⊥AB，CE=EF，AE=AE，

∴△AEF≌△AEC，

∴∠CEA=∠FEA.

∵CD⊥AB，EF⊥AB，

∴CD∥EF，

∴∠FEA=∠CHE.

∵∠FEA=∠CHE，∠CEA=∠FEA，

∴∠CHE=∠CEA，

∴CH=CE.

∵CH=CE，CE=EF，

∴CH=CE=EF.

所以选项B不符合题意；

对于选项D，

∵△AEF≌△AEC，

∴AC=AF.

所以选项D不符合题意.

根据题中条件无法得到CH=HD，

所以选项C符合题意.

故选:C.