题目内容
(本题满分12分)
如图,在平面直角坐标系中,已知抛物线交
轴于
两点,交
轴于点
.
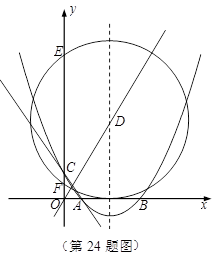
(1)求此抛物线的解析式;
 (2)若此抛物线的对称轴与直线
(2)若此抛物线的对称轴与直线交于点D,作⊙D与x轴相切,⊙D交
轴于点E、F两点,求劣弧EF的长;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
(1)
(2)劣弧EF的长为:
(3)点P坐标为或
时,△PGA的面积被直线AC分成1︰2两部分
解析:(本小题满分12分)
解:(1)∵抛物线经过点
,
,
.
∴, 解得
.
∴抛物线的解析式为:. …………………………3分
(2)易知抛物线的对称轴是.把x=4代入y=2x得y=8,∴点D的坐标为(4,8).
∵⊙D与x轴相切,∴⊙D的半径为8. …………………………4分
连结DE、DF,作DM⊥y轴,垂足为点M.
在Rt△MFD中,FD=8,MD=4.∴cos∠MDF=.
∴∠MDF=60°,∴∠EDF=120°. …………………………6分
![]() ∴劣弧EF的长为:
∴劣弧EF的长为:. …………………………7分
(3)设直线AC的解析式为y=kx+b. ∵直线AC经过点.
∴,解得
.∴直线AC的解析式为:
. ………8分
设点,PG交直线AC于N,
则点N坐标为.∵
.
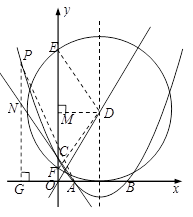 ∴①若PN︰GN=1︰2,则PG︰GN=3︰2,PG=
∴①若PN︰GN=1︰2,则PG︰GN=3︰2,PG=GN.
即=
.
解得:m1=-3, m2=2(舍去).
当m=-3时,=
.
∴此时点P的坐标为. …………………………10分
②若PN︰GN=2︰1,则PG︰GN=3︰1, PG=3GN.
即=
.
解得:,(舍去).当时,
=
.
∴此时点P的坐标为.
综上所述,当点P坐标为或
时,△PGA的面积被直线AC分成1︰2两部分. …………………12分

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案(本题满分12分)
如图, 的顶点A、B在二次函数
的顶点A、B在二次函数 的图像上,又点A、B[来分别在
的图像上,又点A、B[来分别在 轴和
轴和 轴上,
轴上, ∠ABO=
∠ABO= .
.

1.(1)求此二次函数的解析式;(4分)
2.
|
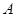 作
作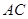 ∥
∥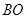 交上述函数图像于点
交上述函数图像于点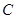 ,
,
点 在上述函数图像上,当
在上述函数图像上,当 与
与 相似时,求点
相似时,求点 的坐标.(8分)
的坐标.(8分)

 的长;
的长;
 与x轴交于A、C两点,与y轴交于B点,与直线
与x轴交于A、C两点,与y轴交于B点,与直线 交于A、D两点。
交于A、D两点。 落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?

 ,
, ,
, .动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
 时,求线段
时,求线段 的长;
的长; 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.