题目内容
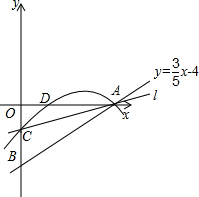 如图,直线y=
如图,直线y=| 3 | 5 |
(1)求B点的坐标;
(2)若D是OA中点,过A的直线l(3)把△AOB分成面积相等的两部分,并交y轴于点C.
①求过A、C、D三点的抛物线的函数解析式;
②把①中的抛物线向上平移,设平移后的抛物线与x轴的两个交点分别为M、N,试问过M、N、B三点的圆的面积是否存在最小值?若存在,求出圆的面积;若不存在,请说明理由.
分析:(1)由直线y=
x-4分别交y轴于B点,令x=0,即可求得B点的坐标;
(2)①由D是OA中点,过A的直线l(3)把△AOB分成面积相等的两部分,并交y轴于点C,即可求得点A,C,D的坐标,然后设过A、C、D三点的抛物线的函数解析式为:y=ax2+bx+c,利用待定系数法即可求得此二次函数的解析式;
②由抛物线的解析式可化为y=-
(x-5)2+
,其对称轴是x=5.由于过M、N的圆的圆心必在对称轴上,要使圆的面积最小,则圆的半径要最小,即点B到圆心的距离要最短,过B作BE垂直抛物线的对称轴,垂足为E,则符合条件的圆是以E为圆心,EB长为半径的圆,求得圆的面积.
| 3 |
| 5 |
(2)①由D是OA中点,过A的直线l(3)把△AOB分成面积相等的两部分,并交y轴于点C,即可求得点A,C,D的坐标,然后设过A、C、D三点的抛物线的函数解析式为:y=ax2+bx+c,利用待定系数法即可求得此二次函数的解析式;
②由抛物线的解析式可化为y=-
| 9 |
| 100 |
| 1 |
| 4 |
解答:解:(1)∵当x=0时,y=-4,
∴B点的坐标为(0,-4);
(2)①∵过A的直线l(3)把△AOB分成面积相等的两部分,
∴C(0,-2),
又∵A(
,0),D是OA中点,
∴D(
,0),
设过A、C、D三点的抛物线的函数解析式为:y=ax2+bx+c,
∴
,
解得:
,
∴过A、C、D三点的抛物线的函数解析式为y=-
x2+
x-2;
②存在.
理由如下:抛物线的解析式可化为y=-
(x-5)2+
,其对称轴是x=5.
由于过M、N的圆的圆心必在对称轴上,要使圆的面积最小,则圆的半径要最小,
即点B到圆心的距离要最短,过B作BE垂直抛物线的对称轴,垂足为E,
则符合条件的圆是以E为圆心,EB长为半径的圆,
其面积为25π.
∴B点的坐标为(0,-4);
(2)①∵过A的直线l(3)把△AOB分成面积相等的两部分,
∴C(0,-2),
又∵A(
| 20 |
| 3 |
∴D(
| 10 |
| 3 |
设过A、C、D三点的抛物线的函数解析式为:y=ax2+bx+c,
∴
|
解得:
|
∴过A、C、D三点的抛物线的函数解析式为y=-
| 9 |
| 100 |
| 9 |
| 10 |
②存在.
理由如下:抛物线的解析式可化为y=-
| 9 |
| 100 |
| 1 |
| 4 |
由于过M、N的圆的圆心必在对称轴上,要使圆的面积最小,则圆的半径要最小,
即点B到圆心的距离要最短,过B作BE垂直抛物线的对称轴,垂足为E,
则符合条件的圆是以E为圆心,EB长为半径的圆,
其面积为25π.
点评:此题考查了函数与点的关系,待定系数法求二次函数的解析式,以及圆的面积的最小问题.此题综合性较强,难度较大,解题的关键是方程思想与数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
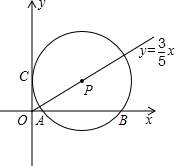 都在直线l上?若存在,请求出直线l的解析式;若不存在,请说明理由.
都在直线l上?若存在,请求出直线l的解析式;若不存在,请说明理由.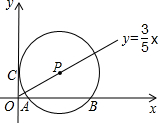 点都在直线l上?若存在,请求出直线l所对应的函数关系式;若不存在,请说明理由.
点都在直线l上?若存在,请求出直线l所对应的函数关系式;若不存在,请说明理由. 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程 ≥
≥