题目内容
如图,P是射线y=| 3 | 5 |
(1)若⊙P的半径为5,则P点坐标是
(2)在(1)的条件下,上述抛物线是否经过点C关于原点的对称点D,请说明理由;
(3)试问:是否存在这样的直线l,当P在运动过程中,经过A、B、C三点的抛物线的顶点
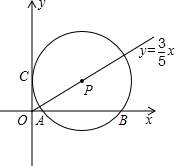 都在直线l上?若存在,请求出直线l的解析式;若不存在,请说明理由.
都在直线l上?若存在,请求出直线l的解析式;若不存在,请说明理由.
分析:(1)如果圆的半径为5,那么P点的横坐标为5,可根据直线O的解析式求出P点的横坐标,连接PA,过P作PQ⊥BA于M,那么PQ=OC,由此在直角三角形OPQ中,根据圆的半径和P点的纵坐标求出AM的长,即可求出A点的坐标,然后用顶点式二次函数通式设抛物线的解析式来设抛物线的,然后将A点坐标代入其中即可求出抛物线的解析式.
(2)由题意可知:D点必在y轴上,因此可根据(1)的抛物线的解析式求出其与y轴的交点,即可判断出D点是否在抛物线上.
(3)可仿照(1)的解题过程进行求解.可先根据直线OP的解析式设出P点的坐标,然后用P点的横坐标仿照(1)的方法求出A,B两点的坐标,然后用待定系数法求出过A,B,C三点的抛物线的解析式,求出其顶点坐标,根据这个顶点坐标即可得出所求的直线解析式.
(2)由题意可知:D点必在y轴上,因此可根据(1)的抛物线的解析式求出其与y轴的交点,即可判断出D点是否在抛物线上.
(3)可仿照(1)的解题过程进行求解.可先根据直线OP的解析式设出P点的坐标,然后用P点的横坐标仿照(1)的方法求出A,B两点的坐标,然后用待定系数法求出过A,B,C三点的抛物线的解析式,求出其顶点坐标,根据这个顶点坐标即可得出所求的直线解析式.
解答:解:(1)P(5,3);
A(1,0);
y=-
(x-5)2+3.
(2)C点关于原点的对称点D的坐标为(0,-3),
∵抛物线y=-
(x-5)2+3与y轴的交点(0,-
),
∴D点不在抛物线y=-
(x-5)2+3上.
(3)设P(m,n),m>0,则n=
m,
过点P作PQ⊥AB,垂足为Q,则AQ=BQ,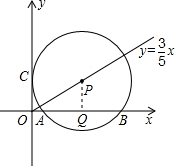
∵PA=PC=m,PQ=
m,
∴AQ=
m,
∴A(
m,0),B(
m,0),C(0,
m),
设经过A,B,C三点的抛物线的解析式为y=a(x-
m)(x-
m),
将C(0,
)代入解析式,
得a=
,
∴y=
(x-
m)(x-
m)
=
(x2-2mx+
m2)
=
[(x-m)2-
m2]
∴y=
(x-m)2-
m
∴抛物线的顶点坐标为(m,-
m)
∴存在直线l:y=-
x,
当P在射线y=
x上运动时,过A,B,C三点的抛物线的顶点都在直线上.
A(1,0);
y=-
| 3 |
| 16 |
(2)C点关于原点的对称点D的坐标为(0,-3),
∵抛物线y=-
| 3 |
| 16 |
| 27 |
| 16 |
∴D点不在抛物线y=-
| 3 |
| 16 |
(3)设P(m,n),m>0,则n=
| 3 |
| 5 |
过点P作PQ⊥AB,垂足为Q,则AQ=BQ,

∵PA=PC=m,PQ=
| 3 |
| 5 |
∴AQ=
| 4 |
| 5 |
∴A(
| 1 |
| 5 |
| 9 |
| 5 |
| 3 |
| 5 |
设经过A,B,C三点的抛物线的解析式为y=a(x-
| 1 |
| 5 |
| 9 |
| 5 |
将C(0,
| 3m |
| 5 |
得a=
| 5 |
| 3m |
∴y=
| 5 |
| 3m |
| 1 |
| 5 |
| 9 |
| 5 |
=
| 5 |
| 3m |
| 9 |
| 25 |
=
| 5 |
| 3m |
| 16 |
| 15 |
∴y=
| 5 |
| 3m |
| 16 |
| 15 |
∴抛物线的顶点坐标为(m,-
| 16 |
| 15 |
∴存在直线l:y=-
| 16 |
| 15 |
当P在射线y=
| 3 |
| 5 |
点评:本题着重考查了待定系数法求二次函数解析式、垂径定理、切线的性质等知识点,综合性强,考查学生数形结合的数学思想方法.

练习册系列答案
相关题目
 24、如图,C是射线OE上的一动点,AB是过点C的弦,直线DA与OE的交点为D,现有三个论断:①DA是⊙O的切线;②DA=DC;③OD⊥OB.请你以其中的两个论断为条件,另一个论断为结论,用序号写出一个真命题,用“★★?★”表示.并给出证明.我的命题是:
24、如图,C是射线OE上的一动点,AB是过点C的弦,直线DA与OE的交点为D,现有三个论断:①DA是⊙O的切线;②DA=DC;③OD⊥OB.请你以其中的两个论断为条件,另一个论断为结论,用序号写出一个真命题,用“★★?★”表示.并给出证明.我的命题是: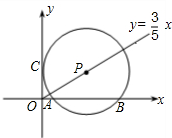 如图,P是射线y=
如图,P是射线y=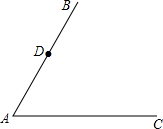 如图,D是射线AB上一点,过点D作DE∥AC,交∠BAC平分线于E,过点D作DF⊥AE,垂足为F.
如图,D是射线AB上一点,过点D作DE∥AC,交∠BAC平分线于E,过点D作DF⊥AE,垂足为F.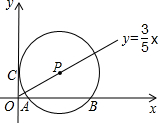 点都在直线l上?若存在,请求出直线l所对应的函数关系式;若不存在,请说明理由.
点都在直线l上?若存在,请求出直线l所对应的函数关系式;若不存在,请说明理由.