题目内容
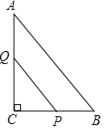
【题目】如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在边BC、AC上,PQ∥AB,把△PCQ绕点P旋转得到△PDE(点C、Q分别与点D、E对应),点D落在线段PQ上,若AD平分∠BAC,则CP的长为_________.
【答案】2
【解析】
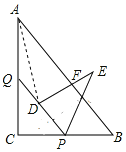
连接AD,根据PQ∥AB可知∠ADQ=∠DAB,再由点D在∠BAC的平分线上,得出∠DAQ=∠DAB,故∠ADQ=∠DAQ,AQ=DQ.在Rt△CPQ中根据勾股定理可知,AQ=12-4x,故可得出x的值,进而得出结论.
连接AD,
∵PQ∥AB,
∴∠ADQ=∠DAB,
∵点D在∠BAC的平分线上,
∴∠DAQ=∠DAB,
∴∠ADQ=∠DAQ,
∴AQ=DQ,
在Rt△ABC中,∵AB=5,BC=3,
∴AC=4,
∵PQ∥AB,
∴△CPQ∽△CBA,
∴CP:CQ=BC:AC=3:4,设PC=3x,CQ=4x,
在Rt△CPQ中,PQ=5x,
∵PD=PC=3x,
∴DQ=2x,
∵AQ=4-4x,
∴4-4x=2x,解得x=![]() ,
,
∴CP=3x=2;
故答案为:2.

练习册系列答案
相关题目