题目内容
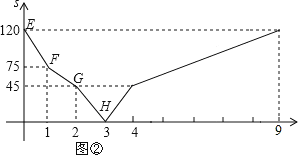
【题目】如图①,在矩形 ABCD中,AB=30cm,BC=60cm.点P从点A出发,沿A→B→C→D路线向点D匀速运动,到达点D后停止;点Q从点D出发,沿 D→C→B→A路线向点A匀速运动,到达点A后停止.若点P、Q同时出发,在运动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象.

(1)请解释图中点H的实际意义?
(2)求P、Q两点的运动速度;
(3)将图②补充完整;
(4)当时间t为何值时,△PCQ为等腰三角形?请直接写出t的值.
【答案】(1)图中点H的实际意义:P、Q两点相遇;(2) P点速度为30cm/s,Q点速度为15cm/s;(3)补图见解析;(4)t=![]() 或t=5或t=8秒时,△PCQ为等腰三角形.
或t=5或t=8秒时,△PCQ为等腰三角形.
【解析】
试题分析:(1)根据P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象得出H点时两点相遇;
(2)利用函数图象得出当两点在F点到G点两点路程随时间变化减慢得出此时Q点停留,只有P点运动,再利用纵坐标的值得出P点和Q点运动速度;
(3)根据4秒后,P点到达D点,只有Q点运动,根据运动速度为15cm/s,还需要运动120-45=75(cm),则运动时间为:75÷15=5(s),进而画出图象即可;
(4)根据Q,P的位置不同,进行分类讨论得出答案即可.
试题解析:(1)图中点H的实际意义:P、Q两点相遇;
(2)由函数图象得出,当两点在F点到G点两点路程随时间变化减慢得出此时Q点停留1秒,只有P点运动,此时纵坐标的值由75下降到45,
故P点运动速度为:30cm/s,再根据E点到F点S的值由120变为75,根据P点速度,得出Q点速度为120-75-30=15(cm/s),
即P点速度为30cm/s,Q点速度为15cm/s;
(3)如图所示:根据4秒后,P点到达D点,只有Q点运动,根据运动速度为15cm/s,
还需要运动120-45=75(cm),则运动时间为:75÷15=5(s),画出图象即可;
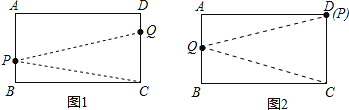
(4)如图1所示,
当QP=PC,此时![]() QC=BP,即30-30t=
QC=BP,即30-30t=![]() (30-15t),
(30-15t),
解得:t=![]() ,
,
故当时间t=![]() 时,△PCQ为等腰三角形,
时,△PCQ为等腰三角形,
如图2所示,
当D,P重合,QD=QC时,
Q为AB中点,则运动时间为:(15+60+30)÷15+1=8(s),
故当时间t=8s时,△PCQ为等腰三角形.
若PC=CQ
故90-30t=30-15t
解得:t=4
则4+1=5(S)
综上所述:t=![]() 或t=5或t=8秒时,△PCQ为等腰三角形.
或t=5或t=8秒时,△PCQ为等腰三角形.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
